Περιεχόμενα

Κατασκευές. 1

1. Κύκλωμα αυτόματου κουδουνιού που κτυπάει αν φωτίσουμε τη φωτοαντίσταση με lazer  1

2. Κατασκευή ραδιοφώνου χωρίς μπαταρίες. 1

3. Κατασκευή ηλεκτρικού κινητήρα με καρφιά.. 1

4. Σύστημα συναγερμού με δέσμη laser. 1

5. Κατασκευή ηλεκτρονικού ηλεκτροσκοπίου με απλά μέσα.. 1

6. Κατασκευή ρευματοσκόπιου με απλά μέσα.. 1

7. Κατασκευή ηλεκτρονικού χρονομετρητή με τη χρήση Η/Υ. 1

8. Κατασκευή φράγματος περίθλασης. 1

9. Η φυσική στο πεζοδρόμιο – ένας πύραυλος με νερό.. 1

10. Κατασκευή μεγάφωνου και μικρόφωνου με απλά μέσα.. 1

11. Κατασκευή τηλεφώνου. 1

12. Μεταφορά πληροφορίας μέσω δέσμης laser. 1

13. Κατασκευή ηλεκτρικής γεννήτριας. 1

14. Κατασκευή πυκνόμετρου – αραιόμετρου.. 1

15. Οι πυκνωτές από μια άλλη σκοπιά.. 1

16. Μια κατασκευή επίδειξης της διαστολής στερεών. 1

17 Κατασκευή μίας πολύ απλής μηχανής του Ήρωνα.. 1

18 Κατασκευή μίας συσκευής Hofman.. 1

19 Κατασκευή μανόμετρου με απλά υλικά.. 1

20 Κατασκευή αισθητήρα θερμοκρασίας για πολύμετρο -βρασμός. 1

 

Η εργασία αυτή περιλαμβάνει τη μελέτη και την κατασκευή ενός απλού συστήματος ενεργοποίησης ενός κουδουνιού από απόσταση, μέσω δέσμης Laser.

 

	ΥΛΙΚΑ
1	Ένα Laser point
2	ένα ηλεκτρικό κουδούνι
3	μια DIAC BT136
4	μια φωτοαντίσταση
5	μια μπαταρία 4,5V
6	ένα χριστουγεννιάτικο λαμπάκι με θερμοστάτη
7	μια πλακέτα με τρύπες κυκλωμάτων

 

Η κατασκευή βασίζεται σε τρία εξαρτήματα.

Την φωτοαντίσταση:Αυτή είναι ένα δίπολο εξάρτημα που η αντίστασή του μεταβάλλεται ανάλογα με την ένταση του φωτισμού που πέφτει πάνω της. Όσο μεγαλύτερη γίνεται η ένταση του φωτισμού που πέφτει πάνω στη φωτοαντίσταση, τόσο μικραίνει η αντίστασή της.

Το TRIAC.

Είναι ένα τρίπολο που έχει την εξής ιδιότητα. Αν μεταξύ των σημείων 1 και 2 παρεμβληθεί αντίσταση μικρότερη από 130Ω περίπου, τα σημεία 2 και 3 βραχυκυκλώνονται και τότε λέμε ότι το diac έκλεισε. Για ν’ ανοίξει ξανά και η σύνδεση ανάμεσα στα σημεία 2 και 3 να διακοπεί, θα πρέπει το ρεύμα που διαρρέει τον κλάδο 2-3 να μηδενισθεί.

Το Λαμπάκι με διμεταλλικό έλασμα

Αυτό είναι ένα κοινό λαμπάκι το οποίο όμως έχει και ένα διμεταλλικό έλασμα, το οποίο άμα ζεσταθεί, λόγω διαφορετικού θερμικού συντελεστή των μετάλλων από τα οποία αποτελείται, στραβώνει και έτσι διακόπτεται η επαφή και το λαμπάκι σβήνει. Είναι εύκολο να το βρούμε σε μια σειρά από χριστουγεννιάτικα φώτα. Είναι αυτό που αναγκάζει τη σειρά ολόκληρη να αναβοσβήνει.

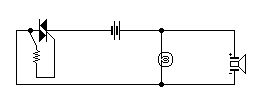
Κύκλωμα αυτομάτου κουδουνιού που κτυπάει για λίγο, αν φωτίσουμε τη φωτοαντίσταση με laser.

Επιστροφή στην αρχή

Το ραδιόφωνο αποτελείται από τα παρακάτω εξαρτήματα

Πηνίο¨:Χάλκινο σύρμα για πηνία γαλβανιζέ διαμέτρου 0,16mm.

Πυρήνας: ξύλινος κύλινδρος διαμέτρου 2,5cm και μήκους 12,5cm.

Δρομέας: Σκληρό μεταλλικό έλασμα περίπου 12,5cm επί 1cm.

Βάση: Ξύλινη με διαστάσεις 20cm επί 20cm επί 1cm.

Πυκνωτής: Πυκνωτής μίκας 0,002mF.

Κρυσταλλικός φωρατής: Δίοδος γερμανίου 1Ν34Α.

Κεραία: Σύρμα από 1,5 έως 3 μέτρα μονωμένο.

Ακουστικά: Ένα ζευγάρι ψηλής εμπέδησης 2000Ω. Αν δε διατίθενται, τότε χρησιμοποιήστε τα κοινά ακουστικά ραδιοφώνου.

Υπόλοιπα υλικά: Βίδες, κορκοδειλάκια, ροδέλες, καρφάκια, τρυπάνι, κολλητήρι, γυαλόχαρτο, μονωτική ταινία.

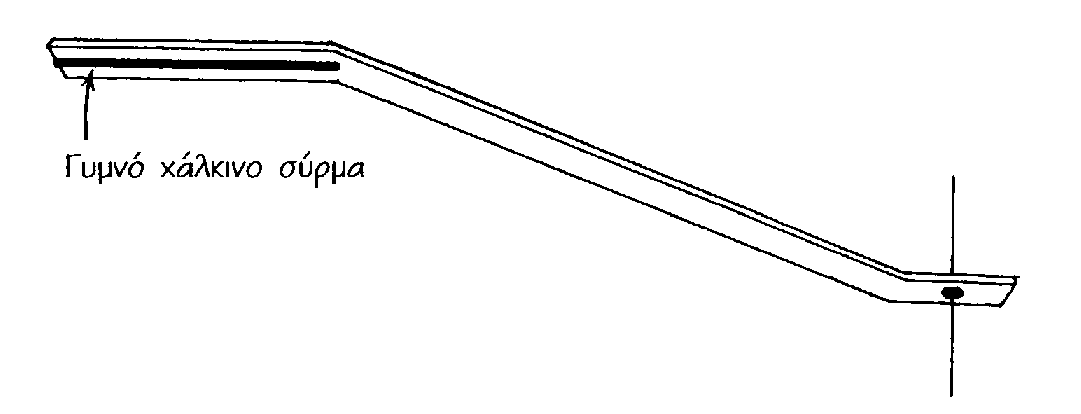
Οδηγίες κατασκευής

Για τον *πυρήνα** αν δεν μπορέσετε να βρείτε ξύλινο κύλινδρο διαμέτρου 2,5cm, μπορείτε να κόψετε το ξύλινο χέρι από κάποια παλιά σκούπα, ή ένα κομμάτι λάστιχο ποτίσματος εξωτερικής διαμέτρου 2,5cm. Αν βρείτε τον κατάλληλο πυρήνα, κόψτε τον σε μήκος 12,5cm, μετρήστε 1 cm από το κάθε άκρο του και βάλτε ένα σημάδι. Στη συνέχεια κάντε μια τρύπα στα σημάδια, διαπερνώντας όλο τον πυρήνα. Αυτές οι τρύπες θα κρατήσουν το εμαγιέ χάλκινο σύρμα στη θέση του. Περάστε περίπου 10cm σύρμα από τη μία τρύπα και αρχίστε να τυλίγετε το πηνίο. Οι σπείρες πρέπει να είναι πυκνές. Θα τυλίξετε περίπου 70 σπείρες, έως ότου φθάσετε στην άλλη σπείρα. Όταν τη φθάσετε, περάστε το σύρμα από αυτήν και κόψτε το αφήνοντας περίπου 10cm. Τρίψτε με ένα γυαλόχαρτο τη μόνωση από το επάνω μέρος του πηνίου, ώσπου να φανεί το γυμνό μέταλλο. Ο δρομέας θα πρέπει να μπορεί να κάνει ηλεκτρική επαφή με κάθε σπείρα του σύρματος του πηνίου.

Για το δρομέα. Κάμψτε το μεταλλικό έλασμα, όπως φαίνεται στο σχήμα. Ένα χοντρό κομμάτι γυμνού χάλκινου σύρματος πρέπει να συγκολληθεί στην κάτω όψη του μπροστινού μέρους. Αυτό το σύρμα επιτρέπει στο βραχίονα να κάνει επαφή το πολύ με 1-2 σπείρες του σύρματος του πηνίου. Αυτό είναι σημαντικό για μια καλή ρύθμιση. Μπορείτε για αυτό το σκοπό να χρησιμοποιήσετε ένα κομμάτι σύρματος εμαγιέ, αν ξύσετε τελείως το βερνίκι του. Τελειώστε το δρομέα τυλίγοντας μονωτική ταινία γύρω από το μπροστινό άκρο, ώστε να εμποδίζεται η επαφή των χεριών σας με το γυμνό μέταλλο, η οποία θα εξασθένιζε αρκετά το σήμα.

Σημ. Το ραδιόφωνο που θα κατασκευάσετε θα πιάνει σταθμούς στα ΑΜ. Για τη λειτουργία του δε χρειάζονται μπαταρίες. Εξήγηση της λειτουργίας του ραδιοφώνου.

Η εξήγηση της λειτουργίας του ραδιοφώνου είναι αρκετά δύσκολη, αφού γι’ αυτήν απαιτούνται γνώσεις απ’ όλα σχεδόν τα κεφάλαια της φυσικής, όπως ηλεκτρισμός, ταλαντώσεις και συντονισμός, κύματα κτλ. Θα επιχειρήσουμε όμως μια απλή όσο το δυνατό εξήγηση.Το βασικό τμήμα του ραδιοφώνου μας είναι ένα κύκλωμα L-C, δηλαδή ένας ηλεκτρομαγνητικός ταλαντωτής. Ο ταλαντωτής αυτός ταλαντώνεται με κάποια συχνότητα που λέγεται ιιδιοσυχνότητα και ισούται με

f=12πL⋅C

Η ιδιοσυχνότητα αυτή αλλάζει, όταν μετακινούμε το δρομέα, αφού η μετακίνηση του δρομέα αλλάζει τον αριθμό των σπειρών του πηνίου, άρα και την αυτεπαγωγή του. Στην κεραία του ραδιοφώνου φθάνουν κύματα διαφόρων συχνοτήτων από τους διάφορους σταθμούς της περιοχής μας. Έτσι το κύκλωμα του ταλαντωτή εκτελεί εξαναγκασμένη ταλάντωση, με αποτέλεσμα να έχουμε το φαινόμενο του συντονισμού. Δηλαδή ο ταλαντωτής θα ταλαντώνεται επιλεκτικά με τη συχνότητα του σταθμού που είναι ίση με την ιδιοσυχνότητά του. Μόνο η ενέργεια του σταθμού που έχει συχνότητα ίση με τη συχνότητα του ταλαντωτή του ραδιοφώνου θα μπορεί να απορροφηθεί από τον ταλαντωτή, θέτοντάς τον σε εξαναγκασμένη ταλάντωση. Η δίοδος θα κάνει αυτό που λέμε αποδιαμόρφωση του σήματος, δηλαδή θα αποκόψει τις αρνητικές ημιπεριόδους, αφού λειτουργεί ως ηλεκτρονική βαλβίδα, αφήνοντας το ρεύμα να περάσει μόνο προς τη μία κατεύθυνση. Τα ακουστικά θα μετατρέψουν τις αργές μεταβολές του ρεύματος, δηλαδή την περιβάλλουσα, σε αντίστοιχες μηχανικές ταλαντώσεις, δηλαδή σε ήχο.**

Επιστροφή στην αρχή

Υλικά που απαιτούνται:

• 30 μετρά χάλκινο σύρμα για πηνία No 26
• 30 μέτρα μονωτική ταινία
• καρφιά 10cm
• καρφιά 6cm
• 2 διχαλωτά καρφιά
• 2 πλατυκέφαλα καρφιά
• 1 κομμάτι ξύλο

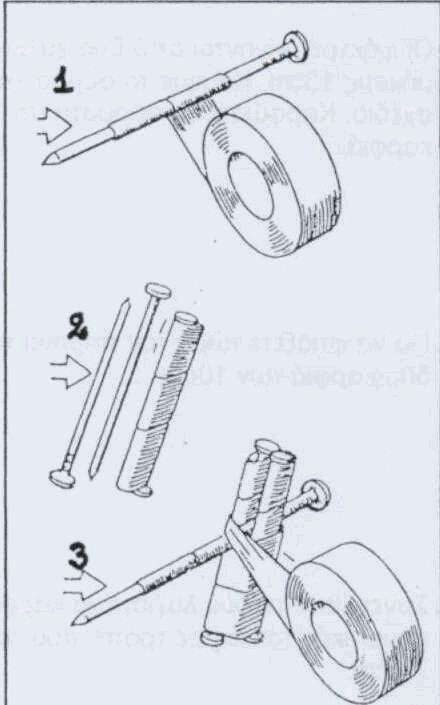
• Για άξονα χρησιμοποιείστε ένα καρφί μήκους 10cm και τυλίξτε γύρω του και επί μήκους 5cm δύο στρώσεις μονωτικής ταινίας
• Ο οπλισμός κατασκευάζεται από δύο ζεύγη καρφιών των 6cm τοποθετημένων έτσι ώστε η μύτη του ενός να βρίσκεται πλάι στο κεφάλι του άλλου και τυλιγμένων με μια στρώση μονωτικής ταινίας
• Από το ένα και το άλλο μέρος του καρφιού που έχετε για άξονα, και σε απόσταση 2,5cm από το κεφάλι του, στερεώστε τα δύο ζεύγη των καρφιών που έχετε προετοιμάσει για οπλισμό, περιτυλίγοντας τα καθ' όλο το μήκος τους με δύο στρώσεις μονωτικής καρφιά αυτά πρέπει να απέχουν εξίσου από κάθε πλευρά του άξονα

 

 

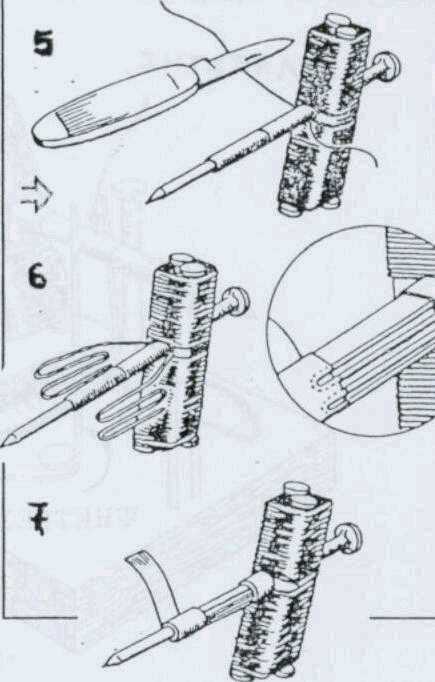
• Περιτυλίξτε στον οπλισμό δύο στρώσεις σύρματος Αφήστε ελεύθερη μια άκρη από το σύρμα, ένα κομμάτι περίπου 18cm, και αρχίστε το τύλιγμα από τη μέση του οπλισμού, δηλαδή από τον άξονα με κατεύθυνση προς τα έξω. Όταν φθάνοντας στην άκρη συμπληρωθεί η πρώτη στρώση του μισού οπλισμού, πρέπει τότε να τυλίξετε αντίστροφα προς τα μέσα και όταν πάλι φθάσετε στη μέση, στον άξονα, πρέπει να περάσετε στο άλλο μισό και να συνεχίσετε να τυλίγετε προς τα έξω, μέχρις ότου φθάσετε στην άλλη άκρη Ύστερα ξαναγυρίστε προς την αντίθετη κατεύθυνση, προς τα μέσα και όταν φθάσετε στον άξονα, κόψτε το σύρμα αφήνοντας πάλι ελεύθερη μια άκρη του 18cm.
• Μ' ένα σουγιά ξυστέ και αποκολλήστε προσεκτικά σε μήκος 15cm το μονωτικό περίβλημα από τις δύο άκρες του σύρματος που αφήσατε ελεύθερες.
• Πριν κατασκευαστεί ο συλλέκτης λυγιστέ τις δύο ελεύθερες άκρες του c σύρματος που απογυμνώσατε και πιέστε τες πάνω στον άξονα και στο σημείο που αρχικά έχετε τυλίξει τη μονωτική ταινία. Προσέξτε ώστε ο οπλισμός να στέκεται κατακόρυφα και τα απογυμνωμένα σύρματα του συλλέκτη να ακουμπούν πάνω στις πλευρές.
• Στερεώστε τα δύο αυτά σύρματα πάνω στον άξονα με δύο κομμάτια στενής μονωτικής ταινίας.
• Για τα υποστηρίγματα που πάνω τους θα τοποθετηθεί ο άξονας, χρησιμοποιήστε 4 καρφιά μήκους 7,5cm καρφώνοντας τα ανά δύο στη ξύλινη βάση. Τα υποστηρίγματα σχηματίζονται από τέσσερις περιελίξεις σύρματος γύρω στις πάνω άκρες των καρφιών. Τα καρφιά και τα στηρίγματα πρέπει να μονταριστούν έτσι ώστε ο οπλισμός να μπορεί να περιστρέφεται εύκολα, ακριβώς στο μέσον μεταξύ των δύο πόλων του ηλεκτρομαγνήτη.
• Οι ψήκτρες γίνονται από δύο χάλκινα σύρματα χωρίς μονωτικό περίβλημα μήκους 15cm. Κάμψτε το σύρμα και δώστε του το σχήμα που δείχνει το σχέδιο. Καρφώστε τα σύρματα στη ξύλινη βάση με δύο πλατυκέφαλα καρφιά
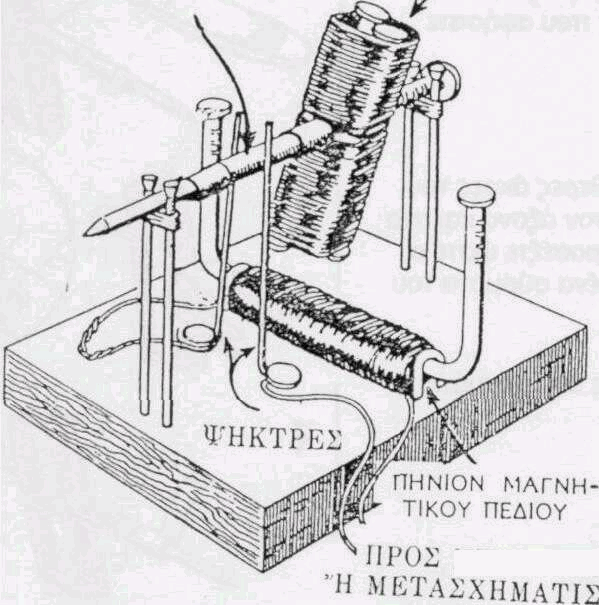
• Για να φτιάξετε τώρα τον πυρήνα του μαγνητικού πεδίου, λυγίστε στη μέση δύο καρφιά των 10cm Συνενώστε τα δύο λυγισμένα καρφιά από τις μύτες τους, με δύο στρώσεις μονωτικής ταινίας με τρόπο που τα κεφάλια τους να απέχουν μεταξύ τους 7,5cm.
• Τυλίξτε γύρω από τον πυρήνα 400 σπείρες χάλκινου σύρματος.
• Αφήστε τα περισσέψει από κάθε άκρη μήκος 10cm.Στερεώστε το μαγνητικό πεδίο στη ξύλινη βάση με δύο δυχαλωτά καρφιά.

 

Επιστροφή στην αρχή

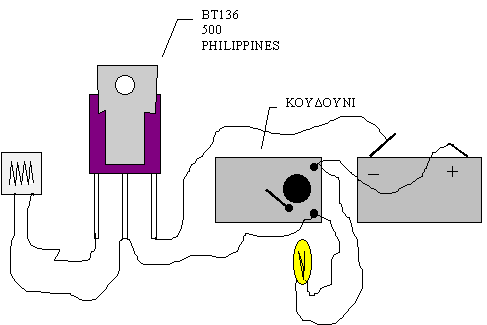
Αυτόματο άναμμα φώτων όταν βραδιάζει

Υλικά που απαιτούνται

Α/Α	ΥΛΙΚΑ
1	Ένα Laser point
2	Ένα triak BD128
3	Ένα μπουτόν
4	Ένα ρελέ με διπλές επαφές των 4.5V
5	Μια φωτοαντίσταση
6	Ένα κύκλωμα τυπωμένων board
	ΣΥΝΟΛΟ

 

Η λειτουργία του συστήματος συναγερμού είναι αρκετά απλή. Το ρελέ το χρησιμοποιούμε ως πύλη ΝΟΤ. Δηλαδή, κλείνοντας το κύκλωμα και πέφτοντας η δέσμη Laser πάνω στη φωτοαντίσταση, η τιμή της αντίστασης γίνεται πολύ μικρή, το ρελέ διεγείρεται και έτσι η πύλη του TRIAK δε διαρρέεται από ρεύμα. Το TRIAK βρίσκεται σε αποκοπή και το λαμπάκι ή το κουδούνι είναι σβηστά.Αν κάτι παρεμβληθεί ανάμεσα στη δέσμη Laser και στη φωτοαντίσταση, η φωτοαντίσταση παύει να φωτίζεται και η αντίστασή της αυξάνει αρκετά. Τότε το ρελέ δε διαρρέεται από αρκετό ρεύμα και έτσι αποδιεγείρεται. Όταν όμως αποδιεγείρεται το ρελέ, η πύλη του Triak διαρρέεται από ρεύμα και το TRIΑΚ γίνεται αγώγιμο. Τότε το λαμπάκι ή το κουδούνι διαρρέονται από ρεύμα.Το TRIAK θα μείνει σ' αυτή την κατάσταση ακόμη και εάν το ρελέ κλείσει και η πύλη του TRIAK σταματήσει να διαρρέεται από ρεύμα. Για να σταματήσει ο συναγερμός, θα πρέπει να διακόψουμε προσωρινά το ρεύμα που διαρρέει το triak, πατώντας το μπουτόν.

 

Για να μην τελειώνει γρήγορα η μπαταρία τόσο στο κύκλωμα του συναγερμού όσο και στο Laser, μπορούμε να χρησιμοποιήσουμε ένα απλό τροφοδοτικό των 4,5V που η τιμή του είναι γύρω στις 1.000 δρχ. Για την τροφοδοσία του Laser ξεβιδώνουμε τη βάση του και αφαιρούμε τις τρεις μικρές μπαταρίες που έχει και συνδέουμε προσεκτικά και με τη σωστή πολικότητα τα άκρα του τροφοδοτικού.Το ίδιο κύκλωμα μπορεί να χρησιμοποιηθεί και ως αυτοματισμός με τον οποίο ν’ ανάβει κάποιο φως, όταν βραδιάζει. Η μόνη μετατροπή που θα κάνουμε είναι παράλληλα με τη φωτοδίοδο να τοποθετήσουμε ένα γραμμικό ποντεσιόμετρο του 1ΚΩ. Ρυθμίζοντας κατάλληλα το ποντεσιόμετρο, μπορούμε να πετύχουμε τον ελάχιστο φωτισμό που επιθυμούμε, ώστε να ενεργοποιείται το triak και ν’ ανάβει το λαμπάκι.

Επιστροφή στην αρχή

Η ανίχνευση ενός μαγνητικού πεδίου μπορεί να γίνει εύκολα είτε με μια απλή πυξίδα είτε με ένα μαγνητόμετρο. Η ανίχνευση όμως ενός ηλεκτρικού πεδίου δεν γίνεται τόσο εύκολα. Μπορούμε βέβαια να χρησιμοποιήσουμε ένα ηλεκτροσκόπιο. Αυτό όμως παρουσιάζει ορισμένα μειονεκτήματα.. Δεν μπορούμε για παράδειγμα να διακρίνουμε τα δύο είδη των φορτίων.

Με το ηλεκτροσκόπιο που προτείνουμε μπορούμε να εξακριβώσουμε την ύπαρξη ενός ηλεκτρικού πεδίου πλησιάζοντας απλώς το φορτισμένο σώμα στη συσκευή. Αν το σώμα αυτό είναι φορτισμένο τότε μια ενδεικτική λάμπα θα ανάβει με το πλησίασμα στη συσκευή ενώ θα σβήνει με την απομάκρυνση του σώματος. Το αντίθετο θα συμβαίνει με το πλησίασμα ενός ετερώνυμου φορτίου.

ΥΛΙΚΑ ΠΟΥ ΘΑ ΧΡΕΙΑΣΤΟΥΝ.

 

1	Μια μπαταρία 4,5 V
2	Ένα λαμπάκι 0,5W, 6V, ή από χριστουγεννιάτικο δέντρο
3	Ένα τρανζίστορ NPN το BC 547
4	Ένα N – MOSFET το BF 961
5	Ένα κολλητήρι και κόλληση.

 

 

 

Με την συνδεσμολογία που πραγματοποιούμε ουσιαστικά φτιάχνουμε έναν πολύ ευαίσθητο ανιχνευτή ηλεκτρικού πεδίου, αφού μπορεί να αλλάξει η κατάσταση του τρανζίστορ BC 547 και να οδηγηθεί από κόρο στην αποκοπή και αντίστροφα, ανάβοντας ή σβήνοντας αντίστοιχα το λαμπάκι, με μια πολύ μικρή τάση που θα εμφανισθεί στην βάση του MOS-FET.

Το εντυπωσιακό της κατασκευής είναι η μεγάλη διακριτική ικανότητα στα δύο είδη φορτίων. Αν τρίψουμε ένα καλαμάκι με χαρτί, αναπτύσσονται αρνητικά φορτία οπότε όταν πλησιάζουμε το καλαμάκι ανάβει το λαμπάκι ενώ όταν το απομακρύνουμε από την βάση του MOSFET σβήνει. Αντίθετα αν τρίψουμε έναν πλαστικό χάρακα σε σακούλα σαν αυτές που φυλάμε τα τρόφιμα, αναπτύσσονται θετικά φορτία, οπότε όταν πλησιάζουμε τον χάρακα σβήνει το λαμπάκι, ενώ όταν τον απομακρύνουμε ανάβει.

Το κόστος της κατασκευής δεν ξεπερνάει τα 3d

Επιστροφή στην αρχή

Η κατασκευή αυτή αφορά μια συσκευή η οποία μπορεί και ανιχνεύει πολύ μικρά ρεύματα της τάξεως των μΑ.. Έτσι μπορεί να χρησιμοποιηθεί σε πολλά και εντυπωσιακά ποιοτικά πειράματα ηλεκτρισμού. Για παράδειγμα.

1. Αφού ανιχνεύει πολύ μικρά ρεύματα, θα ανιχνεύει και πολύ μεγάλες αντιστάσεις. Έτσι μπορούμε να ανάψουμε ένα λεντ αν συνδέσουμε τα δύο άκρα της συσκευής με μια πολύ μεγάλη αντίσταση όπως η αντίσταση του σώματός μας ή η αντίσταση μιας μολυβιάς ή η αντίσταση του πόσιμου νερού. Μπορούμε έτσι να πραγματοποιήσουμε μια σειρά από εντυπωσιακά πειράματα όπως να φτιάξουμε ένα κύκλωμα από μαθητές οι οποίοι σχηματίζουν έναν κύκλο ακουμπώντας μεταξύ τους τα χέρια τους, ενώ ο πρώτος με τον τελευταίο ακουμπάνε τα άκρα της συσκευής. Αν κάποιο ζευγάρι μαθητών από όλους λύσει τα χέρια του, τότε το κύκλωμα ανοίγει και το λεντ της συσκευής σβήνει. Έτσι φτιάχνουμε ένα «ζωντανό» κύκλωμα. Μπορούμε να ζωγραφίσουμε με ένα μολύβι στο τετράδιο μας μια γραμμή. Αν ακουμπήσουμε την αρχή και το τέλος της γραμμής με τα άκρα της συσκευής μας το λεντ ανάβει. Αν η γραμμή είναι με στυλό ή μαρκαδόρο τότε δεν ανάβει. Αυτό δηλώνει ότι ο γραφίτης είναι καλός αγωγός του ηλεκτρισμού. Το ίδιο μπορούμε να επαναλάβουμε με το νερό οπότε το λεντ ανάβει και με λάδι οπότε θα δούμε ότι το λεντ δεν ανάβει.
2. Μπορούμε να ανιχνεύσουμε αν ένα καλώδιο βρίσκεται σε τάση. Αρκεί να πλησιάσουμε το άκρο που έχουμε σχηματίσει κάποιες σπείρες στο καλώδιο. Τότε λόγω επαγωγικών ρευμάτων το λεντ θα ανάψει.
3. Μπορούμε να διαπιστώσουμε στατικά φορτία. Κρατώντας για παράδειγμα το βασικό άκρο της συσκευής στα χέρια μας και τρίβοντας το πόδι μας στο έδαφος το λεντ ανάβει όσο διαρκεί το τρίψιμο, αφού έτσι δημιουργούνται λόγω στατικών φορτίων ρεύματα.

Με φραγμό μόνο τη φαντασία μας μπορούμε να πραγματοποιήσουμε ένα σωρό από άλλα εντυπωσιακά πειράματα. Πλεονέκτημα της συσκευής είναι το χαμηλό κόστος κατασκευής της αφού δεν ξεπερνάει τα 10 ευρώ.

ΥΛΙΚΑ ΠΟΥ ΑΠΑΙΤΟΥΝΤΑΙ:

1. Τρία «3» Τρανζίστορ BC 547B ή ένα μόνο τρανζίστορ BC 517
2. Αντίσταση R1=1ΜΩ
3. Αντίσταση R2=4.7ΚΩ
4. Αντίσταση R3=220Ω
5. Μπαταρία 4,5V
6. Led κόκκινο
7. Project Board 50x80x8mm κυκλωμάτων
8. Καλώδιο μονόκλινο και δύο κροκοδειλάκια.

 

ΚΑΤΑΣΚΕΥΗ:

Πραγματοποιούμε το παρακάτω κύκλωμα :

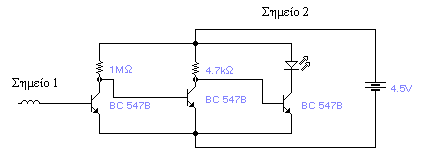
Το άκρο 1 αποτελείται από μονόκλωνο καλώδιο με 25 σπείρες τις οποίες έχουμε φτιάξει με τη βοήθεια ενός στυλό μπικ ως οδηγού.

Στη κατασκευή αυτή φροντίσαμε να χρησιμοποιήσουμε υλικά που υπάρχουν στα σχολεία από το πρόγραμμα PSSC. Μόνο οι τιμές των αντιστάσεων δεν υπάρχουν τις οποίες όμως μπορούμε να προμηθευτούμε από οποιοδήποτε κατάστημα ηλεκτρονικών ανταλλακτικών σε ελάχιστο κόστος όχι μεγαλύτερο των 10 λεπτών.

Την κατασκευή αυτή μπορούμε να την απλοποιήσουμε αρκετά χρησιμοποιώντας ένα μόνο τρανζίστορ τύπου BC336 και ένα λεντ με μικρότερη όμως ευαισθησία. Κολλάμε τον εκπομπό του τρανζίστορ στο αρνητικό της μπαταρίας, το καλώδιο πηνίο στη βάση, και το λεντ με σωστή πολικότητα ανάμεσα στον συλλέκτη και στο θετικό της μπαταρίας. Για να βρούμε τον εκπομπό – βάση – συλλέκτη του τρανζίστορ, το γυρνάμε ανάποδα ώστε να βλέπουμε τα ποδαράκια του και η επίπεδη επιφάνεια να βλέπει το σώμα μας. Τότε τα ποδαράκια είναι από αριστερά προς τα δεξιά εκπομπός-βάση συλλέκτης.

Η κατασκευή μπορεί να γίνει μόνο με ένα τρανζίστορ BC 517 ντάρλινκτον. Την προτείνουμε με τα τρία αφού αυτά τα τρανζίστορ υπάρχουν σε αφθονία στο εργαστήριο.

ΒΙΒΛΙΟΓΡΑΦΙΑ

1. Κυκλώματα Παλμών και Διακοπτών Σ.Α Πακτίτη
2. Εργαστηριακός οδηγός PSSC

 

Επιστροφή στην αρχή

Η μέθοδος που προτείνουμε για τη μέτρηση πολύ μικρών χρόνων είναι πολύ ακριβής και φθηνή. Χρησιμοποιεί την κάρτα ήχου ενός Η/Υ και software το goldwave. ΥΛΙΚΑ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ:

• Μια φωτοαντίσταση
• Μια μπαταρία 4,5 V
• Ένα laser point
• Καλώδιο με δύο κροκοδειλάκια
• Μια αντίσταση 220Ω κόκκινο-κοκκινο-καφέ
• Ένας πυκνωτής 10μF
• Ένα Project Board 50x80x8mm κυκλωμάτων
• Μικροφωνικό καλώδιο 2m μαζί με μονοφωνικό φις
• Ένα βαράκι κρεμασμένο από νήμα
• Η/Υ με κάρτα ήχου

 

Το πρόγραμμα Goldwave είναι freeware μέσω ιντερνετ μπορείτε να το κατεβάσετε και από την ιστοσελίδα του εργαστηριακού κέντρου φυσικών επιστημών κέρκυρας http://web.otenet.gr/ekfekerk

 

ΣΥΝΑΡΜΟΛΟΓΗΣΗ ΤΗΣ ΣΥΣΚΕΥΗΣ:

Η συναρμολόγηση της συσκευής είναι αρκετά εύκολη όπως φαίνεται στο σχήμα. Μπορεί να γίνει χρησιμοποιώντας ένα Project Board χωρίς τη χρήση κολητηριού, η με τη βοήθεια μιας πολύ μικρής διάτρητης πλακέτας και ενός κολητηριού αφού συνολικά χρησιμοποιούμε 3 εξαρτήματα, χωρίς τρανζίστορ διόδους κτλ.

H ανωτέρω διάταξη χρησιμεύει για τη μέτρηση πολύ μικρών χρόνων. Έτσι μπορούμε να μετρήσουμε την περίοδο ενός εκκρεμούς, την συχνότητα περιστροφής ενός μοτέρ κτλ.Μπορούμε ακόμη χρησιμοποιώντας δύο παρόμοιες διατάξεις να μελετήσουμε την ελεύθερη πτώση, την κύλιση σε κεκλιμένο κτλ.Προτείνουμε ακόμη την δημιουργία ειδικού software για την παραπάνω κατασκευή.με την κατασκευή δύο ακριβώς ίδιων κυκλωμάτων και τη σύνδεσή τους παράλληλα, μπορούμε να χρησιμοποιήσουμε το σύστημα για τη μελέτη της ελεύθερης πτώσης, μια μελέτη αρκετά δύσκολη με την βοήθεια χρονομετρητή.Άρα με την ανωτέρω κατασκευή έχουμεμέτρηση συχνότητας κυκλικής κίνησης κινητήρα κτλμέτρηση περιόδου μαθηματικού εκκρεμούςμέτρηση περιόδου ελατηρίουμέτρηση χρόνου ελεύθερης πτώσηςμελέτη ευθύγραμμης ομαλά μεταβαλλόμενης κίνησηςμέτρηση ροπής αδράνειας κυλίνδρου, σφαίρας κτλ

 

Μετρήσεις από την περίοδο ενός μαθηματικού εκκρεμούς

ΒΙΒΛΙΟΓΡΑΦΙΑ

1. Εργαστηριακές Δραστηριότητες Φυσικής Μουρούζης Πάνος Κέρκυρας 1999
2. Κυκλώματα Παλμών και Διακοπτών Σ.Α Πακτίτη
3. Εργαστηριακός οδηγός PSSC*

Επιστροφή στην αρχή

Xρησιμοποιούμε την σχεδίαση του word για να σχεδιάσουμε παράλληλες γραμμές που απέχουν 0,2 mm. Για να το πετύχουμε αυτό από τα εργαλεία σχεδίασης επιλέγουμε συγκράτηση στο πλέγμα και βάζουμε οριζόντια και κατακόρυφη απόσταση 0,02 εκ. όπως φαίνεται στο παρακάτω σχήμα.

 

 

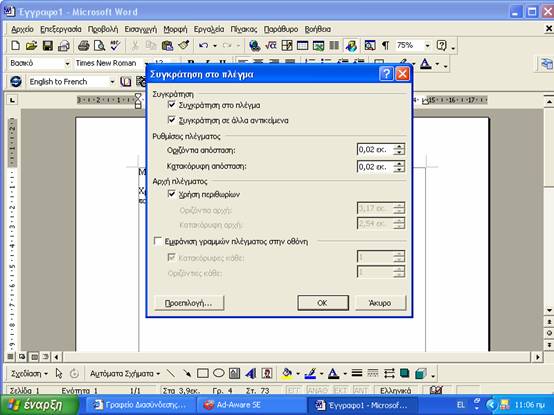
Στη συνέχεια χαράσσουμε μια κατακόρυφη γραμμή και ρυθμίζουμε το πάχος της σε 0,25 στιγμές που είναι και το ελάχιστο πάχος (0,25 στιγμές =0,008527 εκατ ). Θέτουμε το ζουμ στο 500% και πατώντας συγχρόνως τα Shift + Ctrl φέρνουμε παράλληλες ευθείες. Αν δεν τα καταφέρνουμε με τα δύο πλήκτρα τοποθετούμε μια νέα γραμμή πάνω στην προηγούμενη και χρησιμοποιούμε το δεξί βελάκι.Τέλος εκτυπώνουμε σε διαφάνεια με βέλτιστη απόδοση και ασπρόμαυρα. Έχουμε έτσι ένα πολύ ωραίο φράγμα με γνωστό άνοιγμα 0,2mm. Με τη βοήθεια αυτού του φράγματος μπορούμε να υπολογίσουμε το μήκος κύματος μιας δέσμης LASER αλλά και το μέγεθος ενός κυττάρου. Το διάκενο ανάμεσα σε δύο γραμμές είναι0,2-0,08527 χιλ = 0,114 χιλιοστά

Μέτρηση του μεγέθους ενός κυττάρου και του μήκους κύματος δέσμης Laser

Χρησιμοποιώντας το παραπάνω φράγμα μπορούμε να μετρήσουμε το μέγεθος ενός κυττάρου ή το μήκος κύματος μιας ακτίνας Laser.

• Για τη μέτρηση του μεγέθους ενός κυττάρου δουλεύουμε ως εξής: κόβουμε ένα κομμάτι από το φράγμα που φτιάξαμε και το τοποθετούμε ανάμεσα στο δείγμα και στην καλυπτρίδα. Μετρώντας πόσα κύτταρα υπάρχουν ανάμεσα στο διάκενο του φράγματος μπορούμε εύκολα να βρούμε το μέγεθος του κυττάρου.
• για την εύρεση του μήκους κύματος μιαςακτίνας Laser κοιτάξτε τα πειράματα 11 μέτρηση της ταχύτητας του φωτός και 15 εύρεση της χωρητικότητας ενός CD ή DVD

Επιστροφή στην αρχή

Η 26 Ιουνίου έχει καθιερωθεί ως μέρα κατά των ναρκωτικών. Η Ένωση Ελλήνων Φυσικών Παράρτημα Κέρκυρας συμμετείχε στην εκδήλωση με ένα πρόγραμμα από 10 προβλήματα που ζητούσαν τη λύση τους, 10 προτάσεις για απλές και εντυπωσιακές κατασκευές καθώς και μια σειρά από πειράματα επίδειξης. Η εκδήλωση μολονότι πραγματοποιήθηκε στις ημέρες του καύσωνα είχε επιτυχία πέρα από οποιαδήποτε αισιόδοξη πρόβλεψη. Για 3 περίπου ώρες στην πάνω πλατεία της Κέρκυρας ένα σωρό από κόσμο διαφόρων ηλικιών προέλευσης και ιδιοτήτων ασχολήθηκαν με τη φυσική.Μια κατασκευή που είχε μεγάλη επιτυχία περισσότερο στους θεατές μικρής ηλικίας, ήταν ο πύραυλος με νερό που είχαμε κατασκευάσει. Η κατασκευή ήταν πολύ απλή αλλά ταυτόχρονα και εντυπωσιακήΗ ΚΑΤΑΣΚΕΥΗΥλικάΈνα μπουκάλι του νερού 1,5 λίτρωνΈνας πλαστικός φελλός με τρύπα από αυτές που διαθέτει το σχολικό εργαστήριοΜια βαλβίδα αυτοκινήτου ή από τρύπια σαμπρέλα ποδηλάτουΈνας τρίποδας χημείαςΈνα πλαστικό κουτί από ηλιόσπορουςΜια τρόμπα ποδιού

Εργασία

Περνάμε από την τρύπα του φελλού τη βαλβίδα. Αν δεν σφηνώνεται καλά προσθέτουμε λίγη κόλα logo ή σιλικόνη. Προσθέτουμε στο μπουκάλι λίγο νερό. Πχ το 25 % . Σφηνώνουμε το φελλό στο μπουκάλι όσο καλύτερα μπορούμε. Αν ο φελλός είναι αρκετά μεγαλύτερος από τη διάμετρο του μπουκαλιού, τότε ίσως χρειασθεί να τον λειάνουμε με ένα γυαλόχαρτο που θα βρούμε στα χρωματοπωλεία. Ανοίγουμε μια τρύπα στο πλαστικό δοχείο τόση ώστε να περνάει ο λαιμός του μπουκαλιού. Στηρίζουμε το πλαστικό δοχείο στον τρίποδα και το μπουκάλι ανάποδα. Ασφαλίζουμε τη τρόμπα στη βαλβίδα και αρχίζουμε να τρομπάρουμε. Κάποια στιγμή ο φελλός θα φύγει από το μπουκάλι και το μπουκάλι θα εκτιναχθεί προς τα πάνω αρκετά μέτρα (5-10 μέτρα και ακόμη περισσότερο )

 

 

 

ΟΙ ΠΑΡΑΤΗΡΗΣΕΙΣ

Παρατηρήσαμε ότι ο πύραυλός μας ανέβαινε σε μεγάλα ύψη όταν είχε μια συγκεκριμένη ποσότητα νερού περίπου 20% έως 25%. Αν δεν είχε καθόλου νερό ή πολύ νερό, το ύψος που έφθανε ήταν μικρόΠαρατηρήσαμε ακόμη ότι όταν το άδειο μπουκάλι προσγειωνόταν στο έδαφος ήταν θολωμένο από ατμούς που περιείχε.

 

Η ΕΡΜΗΝΕΙΑ

Τις δύο αυτές παρατηρήσεις προσπαθήσαμε να ερμηνεύσουμε. Η πρώτη εργασία που κάναμε ήταν να καταφύγουμε στο internet. Γράψαμε στη μηχανή αναζήτησης του google τις λέξεις « water rocket motion equations » και με μεγάλη μας έκπληξη διαπιστώσαμε ότι αρκετά εκατομμύρια! σελίδες ασχολιόντουσαν με το θέμα αυτό. Ακόμη και το επίσημο site της NASA ασχολείται με αυτή την κατασκευή. Υπάρχουν και αρκετές προσομοιώσεις που βάζοντας τα στοιχεία του πυραύλου μπορούμε να έχουμε το μέγιστο ύψος, τη γραφική παράσταση της ταχύτητας και της επιτάχυνσης κτλ. Στο τέλος του άρθρου παραθέτουμε κατάλογο με μερικές από αυτές τις σελίδες. Έτσι δεν ήταν δύσκολο να βρούμε αυτά που θέλαμε. Την ερμηνεία για τις δύο παρατηρήσεις μας θα τη δώσουμε αρχικά ποιοτικά και στη συνέχεια ποσοτικά.

Ποιοτική ερμηνεία.

Τρομπάροντας τον αέρα που βρίσκεται στο μπουκάλι δίνουμε στον αέρα μια δυναμική ενέργεια. Είναι σαν να συμπιέζουμε ένα φανταστικό ελατήριο. Η ενέργεια αυτή στη συνέχεια μετατρέπεται σε δυναμική και κινητική του νερού καθώς και του άδειου μπουκαλιού. Αν γεμίζαμε το μπουκάλι με νερό δεν θα υπήρχε καθόλου αέρας ώστε να μπορέσουμε να δώσουμε αυτή τη δυναμική ενέργεια με την τρόμπα. Αν από την άλλη μεριά η ποσότητα του νερού ήταν πολύ μικρή, τότε αφενός μεν θα ήταν πολύ μικρή η ορμή που θα δινόταν στο μπουκάλι, αφού η μάζα του αέρα είναι 1000 φορές μικρότερη από τη μάζα του νερού. Η αρχική δυναμική ενέργεια του αέρα μοιράζεται στο νερό και στο μπουκάλι. Όσο μικρότερη η μάζα του μπουκαλιού σε σχέση με αυτή του νερού τόσο μεγαλύτερο ποσοστό ενέργειας θα πάρει. Για παράδειγμα η δυναμική ενέργεια της χορδής ενός τόξου μοιράζεται στο βέλος και στο τόξο-άνθρωπο. Επειδή το βέλος έχει πολύ μικρότερη μάζα από το σύστημα τόξο-άνθρωπος γι αυτό και παίρνει όλη σχεδόν τη δυναμική ενέργεια της χορδής. Αφετέρου ο χρόνος που θα έκανε για να βγει ο συμπιεσμένος αέρας θα ήταν πολύ μικρότερος από αυτόν που κάνει για να φύγει το νερό, αφού το νερό έχει 100 φορές μεγαλύτερο ιξώδες από τον αέρα. Έτσι το διάστημα που θα διάνυε ο πύραυλος θα ήταν αρκετά μικρότερο.Από την άλλη ο αέρας του μπουκαλιού παθαίνει μια αδιαβατική εκτόνωση. Είναι αδιαβατική γιατί συμβαίνει αρκετά γρήγορα, οπότε δεν προλαβαίνει να ανταλλάξει θερμότητα με το περιβάλλον. Στην αδιαβατική όμως εκτόνωση έχουμε ψύξη. Έτσι η θερμοκρασία κατεβαίνει με αποτέλεσμα να υγροποιούνται οι υδρατμοί που περιέχονται στο μπουκάλι και γι αυτό παρατηρούμε το μπουκάλι να θολώνει.

Ποσοτική ερμηνεία.

• P0$P_0$ = η αρχική πίεση στην οποία τρομπάρουμε το μπουκάλι
• Patm$P_{atm}$ = η ατμοσφαιρική πίεση
• V0$V_0$ = ο όγκος του μπουκαλιού
• f$f$= ο συντελεστής πληρότητας με νερό
• m0$m_0$ = η μάζα του μπουκαλιού όταν είναι άδειο
• d$d$ = η πυκνότητα του νερού
• Τπερ$Τ_{περ}$ = η θερμοκρασία περιβάλλοντος
• Τυ$Τ_υ$ = η θερμοκρασία του αέρα όταν φύγει το νερό
• Ττ$Τ_τ$ = η θερμοκρασία του αέρα του μπουκαλιού όταν φύγει και ο επιπλέον αέρας

Εφόσον όπως εξηγήσαμε η μεταβολή του αερίου μπορεί να θεωρηθεί αδιαβατική, το έργο κατά την αδιαβατική εκτόνωση μέχρι να φύγει το νερό θα είναι:

τελτελW=PτελVτελ−PαρχVαρχ1−γ=P⋅V0−P0⋅(1−f)⋅V01−γ$W=\frac{P_{\mathrm{τελ}} V_{\mathrm{τελ}}-P_{αρχ} V_{αρχ}}{1-\gamma}=\frac{P \cdot V_{0}-P_{0} \cdot(1-f) \cdot V_{0}}{1-\gamma}$ (1)

από την εξίσωση Poisson έχουμε:

PV0y=P0⋅(1−f)y⋅V0y→P=P0⋅(1−f)y$P V_{0}^{y}=P_{0} \cdot(1-f)^{y} \cdot V_{0}^{y} \rightarrow P=P_{0} \cdot(1-f)^{y}$ (2)

από τις (1) και (2) προκύπτει ότι :

W=P0⋅V0(1−f)⋅[1−(1−f)γ−1]γ−1$W=\frac{P_{0} \cdot V_{0}(1-f) \cdot\left[1-(1-f)^{\gamma-1}\right]}{\gamma-1}$

το έργο όμως αυτό δεν εκφράζει την κινητική και δυναμική ενέργεια που θα πάρει το μπουκάλι αφού ένα μέρος από αυτή θα πάει και στο νερό. Θα πρέπει να βρούμε το έργο ανά μονάδα αρχικής μάζας, το οποίο θα εκφράζει καλύτερα το πόση ενέργεια θα αποδοθεί τελικά στο μπουκάλι. Έτσι

WmαρX=P0⋅V0(1−f)⋅[1−(1−f)y−1](γ−1)(m0+d⋅f⋅V0)$\frac{W}{m_{\alpha_{\rho_{X}}}}=\frac{P_{0} \cdot V_{0}(1-f) \cdot\left[1-(1-f)^{y-1}\right]}{(\gamma-1)\left(m_{0}+d \cdot f \cdot V_{0}\right)}$

Θα προσπαθήσουμε να βρούμε τώρα βάζοντας τις παρακάτω τιμές να βρούμε για ποιες τιμές του συντελεστή πληρότητας f το έργο ανά μονάδα αρχικής μάζας μεγιστοποιείται.

P0=2Atm=2105N/m2$P_0 = 2Atm =2 105N/m^2$

V0=1,5L=1,510−3m2$V_0 = 1,5L =1,5 10-3m^2$

m0=Kgr$m_0 = Kgr$

d=103Kgr/m3$d = 103 Kgr/m^3$

γ=1,4$γ = 1,4$

 

Wmαρx=750(1−f)⋅[1−(1−f)0,4](0.05+1,5f)$\frac{W}{m_{\alpha \rho_{x}}}=750 \frac{(1-f) \cdot\left[1-(1-f)^{0,4}\right]}{(0.05+1,5 f)}$

 

Κάνοντας τη γραφική παράσταση με τη βοήθεια του προγράμματος DERIVE 6 έχουμε

 

 

Από την παραπάνω γραφική παράσταση φαίνεται ότι το έργο ανά μονάδα μάζας μεγιστοποιείται στο συντελεστή πληρότητας 18% που είναι πολύ κοντά στα πειραματικά μας δεδομένα.Για το θέμα τώρα των ατμών αν εφαρμόσουμε την καταστατική εξίσωση με τις τιμές

P0=Pαρχ=2Atm=2⋅105N/m2$P_0 = P_{αρχ} = 2 Atm = 2\cdot10^5N/m^2$

V0=1,5L(1−f)=80$V_0 = 1,5L(1-f) = 80%1,5 10-3m^2=1,2 10-3m^2$

T0=293K$T_0 =293 K$

---------------------------------------

Pτελ = Pατμ = 1Atm =105N/m2

Vτελ

Tτελ

--------------------------------------

 

Pαρρ⋅VαρJTαρ∄=Pzz⋅VrzTzz→2⋅1,2293=VT→T=122⋅V$\frac{P_{\alpha \rho \rho} \cdot V_{\alpha \rho J}}{T_{\alpha \rho \nexists}}=\frac{P_{\mathrm{zz}} \cdot V_{\mathrm{rz}}}{T_{\mathrm{zz}}} \rightarrow \frac{2 \cdot 1,2}{293}=\frac{V}{T} \rightarrow T=122 \cdot V$

 

από την εξίσωση Poisson έχουμε:

 

PαρXXVαρXy=Prz⋅Vrzy→2⋅1,21,4=V1,4→V=1,2⋅211,4→V=1,968 L$P_{\alpha \rho_{X} X} V_{\alpha_{\rho X}}^{y}=P_{\mathrm{rz}} \cdot V_{\mathrm{rz}}^{y} \rightarrow 2 \cdot 1,2^{1,4}=V^{1,4} \rightarrow V=1,2 \cdot 2^{\frac{1}{1,4}} \rightarrow V=1,968 \mathrm{~L}$

 

Άρα Τ=240Κ→θ=−330C$Τ = 240 Κ \rightarrow θ = -33^0C$

Οπότε έτσι αιτιολογείται η υγροποίηση των υδρατμών του μπουκαλιού.

 

Αναφορές

http://www.fortunecity.com/tattooine/cluster/145/rocket/theory/contents.htm

http://www.impulseaero.com/Software/VCP/index.htmlhttp://www.geocities.com/CapeCanaveral/Lab/5403/http://ourworld.compuserve.com/homepages/pagrosse/h2oRocketIndex.htm

http://ldaps.ivv.nasa.gov/Curriculum/tunnel.html

http://www.npl.co.uk/waterrockets

www.et.byu.edu/~wheeler/benchtop το καλύτερο πρόγραμμα προσομοίωσης του πυραύλου μας

www.smoke.com.au/~ic/water-rocket.html

Bruce R. Munson, Donald F. Young, and Theodore H. Okiishi. Fundamentals of Fluid Mechanics. John Wiley & Sons, 1994.

Mandell, G. et al.:Topics in Advanced Model Rocketry, The MIT Press

Spiegel, M.: Advanced Mathematics, Schaum’s Ouline Series.

Spiegel, M.: Theoretical Mechanics, Schaum’s Ouline Series.

Επιστροφή στην αρχή

ΥΛΙΚΑ ΠΟΥ ΑΠΑΙΤΟΥΝΤΑΙ:

1	Αιωρούμενο πηνίο ΗΛ 190 ή ΗΛ-191
2	Σιδερένιος συμπαγής πυρήνας πχ ένας κυκλικός μαγνήτης από χαλασμένο ηχείο
3	Ένα κουτί από γάλα νουνού
4	Καλώδιο μικροφώνου με βύσμα μικροφώνου
5	Καλώδια με κροκοδειλάκια

ΚΑΤΑΣΚΕΥΗ:

Τοποθετούμε το πηνίο πάνω από τον κυκλικό μαγνήτη ( ο οποίος χρησιμεύει απλά ως πυρήνας για την αύξηση της επαγωγής του πηνίου ) και πάνω από το πηνίο τοποθετούμε το σιδερένιο κουτί από γάλα. Στα άκρα του πηνίου συνδέουμε το σύρμα του μικροφώνου που καταλήγει στο κατάλληλο αρσενικό βύσμα.

 

ΔΟΚΙΜΗ:

Τοποθετούμε το βύσμα στην υποδοχή μεγαφώνου – ηχείων του υπολογιστή μας και βάζουμε να παίξουμε κάποιον ήχο. Ρυθμίζουμε την ένταση ήχου του υπολογιστή στο μέγιστο. Θα πρέπει από το κουτί να ακούγεται καθαρά ο ήχος που παίζεται.

ΕΡΜΗΝΕΙΑ:

 

Η λειτουργία του μεγαφώνου οφείλεται στη δύναμη Laplace. Όταν το πηνίο διαρρέεται από ρεύμα δημιουργεί μεταβαλλόμενο μαγνητικό πεδίο που κάνει το σιδερένιο κουτί να πάλλεται με τον ίδιο ρυθμό. Τον μαγνήτη τον χρησιμοποιούμε απλά ώστε να αυξήσουμε την αυτεπαγωγή του πηνίου. Θα μπορούσαμε αντί για μαγνήτη να χρησιμοποιήσουμε ένα παρόμοιο κομμάτι από σίδηρο.

ΚΑΤΑΣΚΕΥΗ ΜΙΚΡΟΦΩΝΟΥ ΑΝΘΡΑΚΑ ΥΛΙΚΑ ΠΟΥ ΑΠΑΙΤΟΥΝΤΑΙ:

• Μια χαλασμένη μπαταρία των 4,5V
• Μια καλή μπαταρία των 9v με το αντίστοιχο κλιπς της.
• Ένας ηλεκτρολυτικός πυκνωτής 100μF.
• Καλώδιο με βύσμα για μικρόφωνο
• Καλώδια με κροκοδειλάκια
• Κολλητήρι
• Γυαλόχαρτο ή σύρμα κουζίνας χοντρό
• Κόφτη
• Κόλα Logo
• Ένα πλαστικό κουτάκι από καραμέλες όπως στο σχήμα
• Ένα ανταλλακτικό από μολύβι του 1χιλιοστού

 

ΚΑΤΑΣΚΕΥΗ:

Ανοίγουμε με τη βοήθεια κόφτη την μπαταρία των 4,5V και παρατηρούμε ότι αποτελείται από τρία στοιχεία. Κόβουμε με τη βοήθεια του κόφτη το κάθε στοιχείο και αφαιρούμε το καρβουνάκι με προσοχή χωρίς να το σπάσουμε. Το πλένουμε με σαπούνι ώστε να φύγει η πίσσα και το λιμάρουμε με γυαλόχαρτο ή σύρμα κουζίνας ώστε να φανεί καλά το κάρβουνο.

 

Κολλάμε με λόγκο τα δύο κάρβουνα παράλληλα σε απόσταση 4-5cm πάνω στο πλαστικό καπάκι. Τα αφήνουμε αρκετή ώρα ώστε να κολλήσουν καλά.

Παίρνουμε το ανταλλακτικό από μολύβι και το σπάμε στη μέση. Κολλάμε τα δύο κομμάτια παράλληλα σε απόσταση 3cm πάνω στον πάτο του κουτιού ανάποδα όπως στο σχήμα.Στα άκρα από τα δύο κάρβουνα υπάρχει ήδη κολλημένο κομμάτι από χαλκό. Κολλάμε εκεί με τη βοήθεια του κολλητηριού ή με κροκοδειλάκια το κλιπ της μπαταρίας

Στο ένα κάρβουνου κολλάμε με τον ίδιο τρόπο το ένα άκρο από το καλώδιο του μικροφώνου και το άλλο στο άλλο άκρο από το κάρβουνο αφού παρεμβάλλουμε σε σειρά τον πυκνωτή. Το μικρόφωνο είναι έτοιμο.Βάζουμε κάθετα πάνω από τα κάρβουνα το καπάκι με τα μολύβια. Μιλάμε στο μικρόφωνό μας σε απόσταση 2-3 εκατοστά από το καπάκι.

ΔΟΚΙΜΗ:

 

 

Συνδέουμε την μπαταρία.Τοποθετούμε το καπάκι με τα με τα δύο κομμάτια μολυβιού πάνω στα κάρβουνα και κάθετα σε αυτά. Τοποθετούμε το άκρο του μικροφώνου στην υποδοχή για μικρόφωνο του υπολογιστή μας ή στην αντίστοιχη υποδοχή ενός ραδιοκασετόφωνου.Πάμε Έναρξη-Προγράμματα-Βοηθήματα-Πολυμέσα-Ηχογράφηση και δοκιμάζουμε το μικρόφωνο μας μιλώντας 2-3 εκατοστά πάνω από από το καπάκι χωρίς να ακουμπάμε τίποτε άλλο από την κατασκευή μας.

ΕΡΜΗΝΕΙΑ:

Η λειτουργία του μικροφώνου μας βασίζεται ουσιαστικά στο νόμο του Ωμ στο κλειστό κύκλωμα. Μιλώντας πάνω από το καπάκι τα ηχητικά κύματα πιέζουν το καπάκι άρα και τα μολύβια πάνω στα κάρβουνα με μια πίεση που μεταβάλλεται με το χρόνο όπως και η φωνή μας. Έτσι μεταβάλλεται και η αντίσταση του κυκλώματος, αφού όταν η πίεση είναι μεγάλη η αντίσταση του κυκλώματος γίνεται μικρή και το ρεύμα που το διαρρέει μεγάλο. ( η αντίσταση γίνεται μικρή γιατί έχουμε καλύτερη επαφή ανάμεσα στους άνθρακες δηλαδή αυξάνει το εμβαδόν άρα μικραίνει η αντίσταση ). Τοποθετούμε τον πυκνωτή ώστε να κόψουμε την DC συνιστώσα, δηλαδή τα 9V ώστε να περάσει μόνο το εναλλασσόμενο ρεύμα που οφείλεται στις μεταβολές της αντίστασης του κυκλώματος.

ΕΦΑΡΜΟΓΗ:

Μπορούμε χρησιμοποιώντας αυτές τις δύο κατασκευές επί δύο, καθώς και ένα αρκετά μακρύ τετράκλωνο τηλεφωνικό καλώδιο να φτιάξουμε με απλά μέσα ένα τηλέφωνο διπλής επικοινωνίας. Σε αυτή την περίπτωση δεν θα χρησιμοποιήσουμε τον πυκνωτή. Η εμβέλεια του τηλεφώνου μας είναι εντυπωσιακά μεγάλη. Μπορεί να φθάσει και στα 200 - 300 μέτρα. Για την εφαρμογή του καλωδίου θα πρέπει να χρησιμοποιήσουμε κλίπς αμερικάνικου τύπου όπως λέμε.

 

ΒΙΒΛΙΟΓΡΑΦΙΑ

1. Εργαστηριακές Δραστηριότητες Φυσικής Μουρούζης Πάνος Κέρκυρας 1999

Επιστροφή στην αρχή

ΥΛΙΚΑ ΠΟΥ ΘΑ ΧΡΕΙΑΣΤΟΥΜΕ:

1. Δύο μπαταρίες 9 Volt
2. Δύο κλίπς για τις μπαταρίες
3. Δύο μικρά μεγαφωνάκια ( από παλιά τηλέφωνα )
4. Δύο μικρόφωνα άνθρακα ( από παλιά τηλέφωνα )
5. Δύο θηλυκά κλίπς τηλεφωνικού καλωδίου
6. Τηλεφωνικό καλώδιο από 10 μέχρι 30 μέτρα με κλίπς στα δύο άκρα
7. δύο κομμάτια από διάτρητη πλακέτα διαστάσεων 5cm x 17cm το καθένα

ΕΡΓΑΛΕΙΑ ΠΟΥ ΘΑ ΧΡΕΙΑΣΤΟΥΜΕ:

1. κολλητήρι και καλάι
2. θερμόκολλα σιλικόνης ή εναλλακτικά λίγο μονόκλωνο καλώδιο
3. έναν κόφτη
4. έναν γδάρτη καλωδίων ή εναλλακτικά έναν αναπτήρα.

ΤΡΟΠΟΣ ΕΡΓΑΣΙΑΣ:

Κολλάμε πρώτα το μικρόφωνο το μεγάφωνο και το θηλυκό κλιπ με θερμόκολλα σιλικόνης πάνω στην πλακέτα από την μεριά του χαλκού. Αν δεν έχουμε θερμόκολλα μπορούμε να στερεώσουμε αυτά τα εξαρτήματα με άλλη κόλλα ή με ένα μονόκλωνο καλώδιο. Αφού τα στερεώσουμε κάνουμε τις απαραίτητες συνδέσεις όπως φαίνεται στο παραπάνω σχήμα. Οι συνδέσεις γίνονται πάνω στην πλακέτα με καλάι. Τέλος στερεώνουμε τη μπαταρία είτε με ταινία διπλής όψεως είτε με μονόκλωνο καλώδιο. Με τον ίδιο τρόπο κάνουμε και το δεύτερο τηλέφωνο. Προσέξτε ότι οι κατασκευές δεν έχουν τις ίδιες ακριβώς συνδέσεις. Πχ το κίτρινο καλώδιο ενώ στο πρώτο τηλέφωνο συνδέεται με τον αρνητικό πόλο της μπαταρίας, στο δεύτερο συνδέεται με το μικρόφωνο.

Μολονότι το τηλέφωνό μας δεν έχει ενισχυτή η εμβέλειά του είναι πολύ μεγάλη. Στη δική μας κατασκευή ακουγόταν άψογα στα 30 μέτρα που ήταν και το μήκος του καλωδίου μας.

Ερωτήσεις:

1. Ερμηνεύστε τη λειτουργία του μεγαφώνου σύμφωνα με τις αρχές της φυσικής που γνωρίζετε.
2. Ερμηνεύστε τη λειτουργία του μικροφώνου άνθρακα σύμφωνα με τις αρχές της φυσικής που γνωρίζετε.
3. Θα μπορούσαμε να πραγματοποιήσουμε την επικοινωνία των δύο τηλεφώνων με τρία καλώδια αντί με τέσσερα;.
4. Πως τα σύγχρονα τηλέφωνα χρησιμοποιούν δύο καλώδια αντί τέσσερα;
5. Τι περιορίζει την εμβέλεια του τηλεφώνου μας;. Πως θα μπορούσαμε να την αυξήσουμε;

Φωτογραφία του τηλεφώνου μας

Επιστροφή στην αρχή

Είναι αλήθεια αξιοπερίεργο πως με την κατάλληλη έμπνευση και με πολύ απλά και φθηνά υλικά μπορεί κάποιος να δημιουργήσει μια πειραματική διάταξη που να αναδεικνύει πολλά και εντυπωσιακά φαινόμενα από την επιστήμη και την τεχνολογία, προσφέροντας έτσι ένα καταπληκτικό εκπαιδευτικό εργαλείο. Στην συγκεκριμένη κατασκευή καταφέραμε να μεταφέρουμε ένα ηχητικό σήμα μέσω μιας δέσμης Laser χρησιμοποιώντας απλούστατα υλικά και με κόστος μικρότερο από 10€

Υλικα Που Απαιτουνται:

1. Ένα Laser Point
2. Ένα μεγάφωνο από παλιό ακουστικό τηλεφώνου.
3. Καλώδια με κροκοδειλάκια
4. Δύο φωτοαντιστάσεις
5. Μπαταρία 9V με κλίπς
6. Μπαταρία 4,5V
7. Καλώδιο με αντάπτορα για είσοδο μικροφώνου- μεγαφώνου
8. Μετασχηματιστής 220-12 V

Κατασκευη:

Α' Κατασκευή του διαμορφωτή – πομπού.

Βήμα 1ο

Αφαιρούμε το καπάκι από το Laser και συνδέουμε τα δύο καλώδια με τα κροκοδειλάκια το ένα εσωτερικά ώστε να πιάσει στο ελατήριο που περιέχει και το άλλο στο εξωτερικό περίβλημα. Με ένα σελοτέιπ κολλάμε το διακόπτη ώστε να είναι συνεχώς κλειστός. Τώρα το Laser είναι έτοιμο να τροφοδοτηθεί με εξωτερική πηγή – μπαταρία.

Βήμα 2ο

Συνδέουμε σε σειρά με το Laser τον μετασχηματιστή στην είσοδο των 12V και την μπαταρία όπως στο σχήμα. Το καλώδιο με τον αντάπτορα το συνδέουμε στην στο πρωτεύον του μετασχηματιστή στα 220V. Ο πομπός μας είναι έτοιμος να δεχθεί το σήμα από ένα ραδιοκασετόφωνο, ή από την έξοδο ενός Η/Υ από την κάρτα ήχου εκεί που τοποθετούνται τα ηχεία.

Μπορούμε να μεταφέρουμε απευθείας και τη δική μας φωνή αρκεί στη θέση του αντάπτορα να τοποθετήσουμε ένα μικρόφωνο άνθρακα από ακουστικό τηλεφώνου, σε σειρά με μια 9 V μπαταρία.

Β΄ Κατασκευή του αποδιαμορφωτή - δέκτη.

Συνδέουμε σε σειρά την μπαταρία των 9V το μεγάφωνο από το ακουστικό ενός παλιού τηλεφώνου και μια φωτοαντίσταση. Για μεγαλύτερη ευαισθησία μπορούμε να συνδέσουμε δύο φωτοαντιστάσεις σε σειρά. Ο δέκτης μας είναι έτοιμος. Φροντίζουμε ώστε η διαμορφωμένη ακτίνα του Laser να πέφτει πάνω στη δίοδο και το μεγάφωνο να το έχουμε κοντά στο αυτί μας. Θα ακούσουμε πολύ καλά το σταθμό του ραδιοφώνου ή αυτό που παίζει η κάρτα ήχου του υπολογιστή μας, ή τον συνομιλητή μας αν έχουμε επιλέξει την απευθείας λήψη.

 

ΕΞΗΓΗΣΗ ΤΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΤΗΣ ΚΑΤΑΣΚΕΥΗΣ:

Για τον πομπό :

Η τάση που εφαρμόζεται στο Laser είναι η σταθερή τάση καθώς και η από αμοιβαία επαγωγή λόγω του πηνίου. Έτσι θα έχει τη μορφή Vολ=Vστ+Vεν . Έτσι θα είναι μια τάση σταθερή των 4,5V η οποία όμως θα μεταβάλλεται λιγάκι γύρω από την τιμή των 4,5V με τον ίδιο ακριβώς τρόπο που μεταβάλλεται και η φωνή μας. Τα φαινόμενα που εμπλέκονται μέχρι εδώ είναι της αμοιβαίας επαγωγής καθώς και ο 2ος κανόνας του Κίρχωφ. Προφανώς η ένταση ακτινοβολίας του Laser θα μεταβάλλεται με τον ίδιο τρόπο αφού είναι ανάλογη της τάσης τροφοδοσίας του. Αυτό έχει να κάνει και με τη συνθήκη του Borh αφού μεγαλύτερη τάση σημαίνει μεγαλύτερη προσφορά ενέργειας στα ηλεκτρόνια, άρα θα έχουμε περισσότερες διεγέρσεις – αποδιεγέρσεις από τη δίοδο Laser.

Για τον δέκτη:

Λόγω του νόμου του Ωμ στο κλειστό κύκλωμα οι μεταβολές της φωτοαντίστασης που οφείλονται στη μεταβολή της έντασης της δέσμης Laser, μετατρέπονται σε μεταβολές ρεύματος. Το ρεύμα αυτό προκαλεί μεταβαλλόμενο μαγνητικό πεδίο στο πηνίο του μεγαφώνου, το οποίο με τη σειρά του ασκεί δύναμη Laplace πάνω σε μια σιδερένια μεμβράνη του μεγαφώνου. Έτσι η μεμβράνη αυτή πάλλεται όπως ακριβώς μεταβάλλεται το ρεύμα στο κύκλωμα, δημιουργώντας τα ηχητικά κύματα που φθάνουν στο αυτί μας.

Ο ήχος δημιουργείται από μια μηχανική ταλάντωση και μεταδίδεται στον αέρα με μεταβολές της πίεσης του αέρα.

Σημ:

Στον διαμορφωτή πρέπει να προσθέσουμε σε σειρά αντίσταση 10ΚΩ ώστε να αποφύγουμε το κάψιμο του laser από την μεγάλη επαγωγική τάση που αναπτύσσεται λόγω του μετασχηματιστή. Μέχρι να το ανακαλύψουμε αυτό κάψαμε αρκετά laser.

 

Ο πομπός	Ο δέκτης

Επιστροφή στην αρχή

( Με απλά μέσα )

Ο πιο σημαντικός νόμος του Ηλεκτρομαγνητισμού από πρακτική άποψη ( και ίσως και από θεωρητική ) είναι ο νόμος του Φαραντέυ. Και αυτό γιατί ο τρόπος με τον οποίο παράγεται η ηλεκτρική ενέργεια σε όλον τον πλανήτη είναι ένας και μοναδικός, αυτός που βασίζεται πάνω στο νόμο του Φαραντέυ. Σε όλα τα εργοστάσια παραγωγής ηλεκτρικής ενέργειας αυτό που συμβαίνει τελικά είναι να κινείται ένας μαγνήτης κοντά σε ένα πηνίο ή αντιστρόφως. Αν η κίνηση δημιουργείται από καύση κάρβουνου, το εργοστάσιο λέγεται θερμοηλεκτρικό, αν δημιουργείται από έναν καταρράκτη, λέγεται υδροηλεκτρικό, αν δημιουργείται από τη θερμότητα που παράγεται από κάποια πυρηνική αντίδραση λέγεται θερμοπυρηνικό, αν δημιουργείται από τον άνεμο, ανεμογεννήτρια κλπ.

Στην επίδειξη όμως αυτού του νόμου έχουμε το εξής πρόβλημα. Αν κινήσουμε ένα μαγνήτη κοντά σε ένα πηνίο, επειδή η ηλεκτρική ισχύς που παράγεται είναι πολύ μικρή, δεν μπορούμε να ανάψουμε ένα λαμπάκι. Αυτό που κάνουμε είναι να μετακινούμε τη βελόνα από ένα αμπερόμετρο. Αυτό όμως δεν πείθει τους μαθητές ότι η κίνηση αυτή είναι ικανή να παράγει ηλεκτρική ενέργεια. Αν χρησιμοποιήσουμε μία εργοστασιακή ηλεκτρογεννήτρια, δεν φαίνεται ευκρινώς η απλότητα της κατασκευής, αφού χρησιμοποιούνται γρανάζια για τον πολλαπλασιασμό των στροφών κλπ. Σε αυτή την κατασκευή προσπαθήσαμε να λύσουμε τα παραπάνω προβλήματα ως εξής. Αντί για λαμπάκι χρησιμοποιήσαμε ένα Led έτσι ώστε να ανάβει με μικρότερη ισχύ και φροντίσαμε να δώσουμε πολλές στροφές στον μαγνήτη προσαρμόζοντάς τον πάνω σε ένα μιξεράκι για φραπέ.

Τι θα χρειαστούμε:

1. έναν ραβδόμορφο μαγνήτη
2. ένα πηνίο 1200 σπειρών με πυρήνα
3. ένα μιξεράκι για φραπέ
4. ένα λαμπάκι Led ( υψηλής φωτεινότητας καλύτερα)
5. καλώδια με κροκοδειλάκια και λίγο σύρμα

Τι κάνουμε:

1. Στερεώνουμε τον ραβδόμορφο μαγνήτη στο μιξεράκι με τη βοήθεια λίγου σύρματος.
2. Βάζουμε τον πυρήνα στο πηνίο
3. Συνδέουμε το led με τη βοήθεια των καλωδίων στο πηνίο
4. Στρέφουμε τον μαγνήτη κοντά στον πυρήνα και παρατηρούμε ότι το led ανάβει

 

Επιστροφή στην αρχή

Η προσπάθειά μας είναι να κατασκευάσουμε ένα πυκνόμετρο με το οποίο να μπορούμε να μετρήσουμε με μεγάλη ακρίβεια (~ 0,1 %w/v) την περιεκτικότητα ενός διαλύματος NaCl ή ζάχαρης ή αιθυλικής αλκοόλης κλπ. Με άλλα λόγια θέλουμε να κατασκευάσουμε ένα πυκνόμετρο που να έχει μία κατακόρυφη ευσταθή ισορροπία και να μπορεί μία μικρή μεταβολή στην πυκνότητα του διαλύματος να επιφέρει μεγάλη μεταβολή στην ένδειξη του. Για να πετύχουμε αυτό το στόχο μελετάμε θεωρητικά την ισορροπία του.

Έστω ότι το σχήμα του είναι ένας όγκος Vo που είναι πάντα βυθισμένος και ένας λεπτός κύλινδρος μέρος του οποίου βυθίζεται στο διάλυμα. Από τη συνθήκη ισορροπίας του οργάνου σε δύο διαλύματα με διαφορετικές πυκνότητες θα έχουμε:

 

(Vo+Sh)dg=B→(Vo+Sh1)d1g=(Vo+Sh2)d2g→(Vo+Sh1)d1=(Vo+S(h1−x))d2$(V o+S h) d g=B \rightarrow\left(V o+S h_{1}\right) d_{1} g=\left(V o+S h_{2}\right) d_{2} g \rightarrow\left(V o+S h_{1}\right) d_{1}=\left(V o+S\left(h_{1}-x\right)\right) d_{2}$

 

Όπου x η μεταβολή της ένδειξης του οργάνου στα δύο διαλύματα.

Άρα

x=d2−d1d1⋅(h1+VoS)$x=\frac{d_{2}-d_{1}}{d_{1}} \cdot\left(h_{1}+\frac{V_{o}}{S}\right)$

 

Επομένως το x είναι τόσο μεγαλύτερο όσο μεγαλύτερο είναι το Vο και το h1 και όσο μικρότερο είναι το S

 

Για να πετύχουμε τους παραπάνω στόχους χρησιμοποιήσαμε τα υλικά:

1. μία αμπούλα από φυσικό ορό
2. ένα καλαμάκι αναψυκτικού
3. σκάγια μικρά από μόλυβδο
4. μία κλίμακα σε χαρτί (η παρακάτω εικόνα)

Χρησιμοποιήσαμε τα εργαλεία

1. ψαλίδι
2. κόλλα στεγανοποίησης σιλικόνη ή οποιαδήποτε άλλη
3. ογκομετρικό κύλινδρο 100mL
4. καλαμάκι από σουβλάκι

 

Διεργασία

1. Κόβουμε την αμπούλα του ορού με ένα ψαλίδι τόσο όσο να χωράει ίσα ίσα το καλαμάκι.
2. Τοποθετούμε το καλαμάκι μέσα στον ορό και προσθέτουμε τόσα σκάγια ώστε όταν τοποθετήσουμε την αμπούλα με το καλαμάκι μέσα στον ογκομετρικό κύλινδρο με το νερό, να βυθίζεται μεγάλο μέρος του. Αυτό όταν το πυκνόμετρό μας θέλουμε να το χρησιμοποιήσουμε για διαλύματα με μεγαλύτερο ειδικό βάρος από το νερό όπως πχ το ζαχαρόνερο ή το αλατόνερο. Όταν όμως θέλουμε να το χρησιμοποιήσουμε για διαλύματα με μικρότερο ειδκό βάρος από το νερό όπως διαλύματα αλκοόλης, τότε θα πρέπει να βάλουμε τόσα σκάγια ώστε από το καλαμάκι μας να βυθίζεται το μικρότερο μέρος του.
3. Εκτυπώνουμε και κόβουμε την παρακάτω κλίμακα με ένα ψαλίδι, και χρησιμοποιώντας ένα καλαμάκι από σουβλάκι, την τοποθετούμε μέσα στο καλαμάκι για αναψυκτικά που έχουμε βάλει μέσα στην αμπούλα
4. Στεγανοποιούμε το καλαμάκι με την αμπούλα χρησιμοποιώντας την κατάλληλη κόλλα.
5. Με έναν αναπτήρα καίμε λίγο το πάνω μέρος από το καλαμάκι και το σφραγίζουμε ώστε να μην μας φεύγουν τα σκάγια. Το πυκνόμετρο-αραιόμετρό μας είναι έτοιμο.

Επιστροφή στην αρχή

«Μια εκπαιδευτική πρόταση»

Ένας επίπεδος πυκνωτής είναι ένα σύστημα που αποτελείται από δύο παράλληλες μεταλλικές πλάκες ανάμεσα στις οποίες υπάρχει αέρας ή κάποιο μονωτικό υλικό ( διηλεκτρικό).

Γιατί μελετάμε ένα τέτοιο σύστημα στον ηλεκτρισμό; Για τις περίεργες ηλεκτρικές ιδιότητες που παρουσιάζει. Και αυτές είναι δύο

1. Μπορεί και αποθηκεύει μεγάλες ποσότητες ηλεκτρικού φορτίου και μεγάλη ποσότητα ηλεκτρικής ενέργειας. Δηλαδή μοιάζει με μια κονσέρβα ηλεκτρικής ενέργειας.
2. Ενώ αποτελεί εμπόδιο για το σταθερό ρεύμα ( λόγω του διηλεκτρικού ) δεν αποτελεί εμπόδιο για το εναλλασσόμενο ρεύμα.

Σταθερό ρεύμα δημιουργείται από μία σταθερή τάση. Σταθερή τάση παρέχουν οι μπαταρίες. Σε αυτή την περίπτωση το ρεύμα έχει σταθερή ένταση καθώς και σταθερή κατεύθυνση. Εναλλασσόμενο ρεύμα δημιουργείται από εναλλασσόμενη τάση. Εναλλασσόμενη τάση παρέχουν οι πρίζες του σπιτιού μας. Μια τέτοια τάση αλλάζει συνεχώς πολικότητα και περιγράφεται από μία εξίσωση της μορφής V=Voημωt. Η τάση Vo είναι η μέγιστη τιμή της τάσης και λέγεται πλάτος, ενώ η σταθερά ω λέγεται κυκλική συχνότητα.

Αν στους πόλους ενός πυκνωτή εφαρμόσουμε μία σταθερή τάση τότε οι οπλισμοί του θα αποκτήσουν κάποιο φορτίο. Το φορτίο που θα αποκτήσουν είναι ανάλογο της τάσης που εφαρμόσαμε. Το σταθερό πηλίκο Q/V λέγεται χωρητικότητα του πυκνωτή (όπου Q το φορτίο του θετικού οπλισμού). Επιλέξαμε το όνομα χωρητικότητα αφού το μέγεθος αυτό εκφράζει το πόσα φορτία αποκτάει ένας πυκνωτής αν τον φορτίσουμε με δεδομένη τάση. Με άλλα λόγια αν στην ίδια μπαταρία συνδέσουμε διάφορους πυκνωτές, αυτός με τη μεγαλύτερη χωρητικότητα, θα αποκτήσει τα περισσότερα φορτία.

Έτσι ορίσαμε ως χωρητικότητα το μέγεθοςC=QV$C=\frac{Q}{V}$ ( Μονάδες 1C/V=1Farad$1C/V=1Farad$)

 

Λόγω του σχήματος του επίπεδου πυκνωτή επιλέξαμε να συμβολίζουμε τον πυκνωτή γενικά ως -| |-

 

 

Η χωρητικότητα ενός πυκνωτή εξαρτάται από 3 παράγοντες.

1. το εμβαδόν των οπλισμών του πυκνωτή ( ανάλογα)
2. την απόσταση ανάμεσα στους οπλισμούς του πυκνωτή ( αντιστρόφως ανάλογα )
3. το είδος του διηλεκτρικού-μονωτή που υπάρχει ανάμεσα στους οπλισμούς. Ο τέλειος μονωτής έχει άπειρη αντίσταση. Γενικά όμως οι μονωτές μπορεί να παρουσιάζουν μεγάλη αντίσταση όχι όμως άπειρη. Όσο μεγαλύτερη αντίσταση παρουσιάζει ένας μονωτής, τόσο πιο καλός μονωτής θεωρείται. Όσο χειρότερος είναι, δηλαδή όσο μικρότερη αντίσταση παρουσιάζει, τόσο μεγαλύτερη η χωρητικότητα του πυκνωτή. Το πιο καλό μονωτικό είναι ο αέρας. Άρα αν βάλουμε ένα διηλεκτρικό ανάμεσα στους οπλισμούς του πυκνωτή, αφού θα είναι χειρότερος μονωτής από τον αέρα, η χωρητικότητα του πυκνωτή θα είναι μεγαλύτερη. Το πόσες φορές θα μεγαλώσει η χωρητικότητα το ονομάζουμε διηλεκτρική σταθερά του μονωτικού υλικού. Π.χ αν ένας πυκνωτής γεμίσει με νερό, η χωρητικότητά του θα αυξηθεί κατά 81 φορές, άρα το νερό έχει διηλεκτρική σταθερά 81. Το χαρτί 4, το πετρέλαιο 5 κλπ

Όλα τα παραπάνω συνοψίζονται στον τύπο

C=εεoSl$C=\varepsilon \varepsilon_{o} \frac{S}{l}$ ÓTTOU ηλKηλ=14πεo=9⋅109Nm2C2$K_{\text {ηλ}}=\frac{1}{4 \pi \varepsilon_{o}}=9 \cdot 10^{9} \frac{\mathrm{Nm}^{2}}{\mathrm{C}^{2}}$

Θα προσπαθήσουμε τώρα να ερμηνεύσουμε τόσο την πρώτη όσο και την δεύτερη ιδιότητα του πυκνωτή.

Ας υποθέσουμε ότι έχουμε μία μεταλλική πλάκα με φορτίο +Q. Οι δυναμικές γραμμές θα φεύγουν από τη μεταλλική πλάκα προς το άπειρο. Άρα το ηλεκτρικό πεδίο που δημιουργεί η πλάκα θα είναι διασκορπισμένο σε όλο το χώρο. Το ίδιο θα συμβαίνει αν διαθέτουμε και μία μεταλλική πλάκα με φορτίο –Q. Αν όμως πλησιάσουμε τις δύο πλάκες αρκετά κοντά, τότε οι δυναμικές γραμμές θα στραβώσουν και όλες οι δυναμικές γραμμές που φεύγουν από τη θετική πλάκα θα πηγαίνουν στην αρνητική και όχι στο άπειρο, οπτικοποιώντας έτσι την έλξη των δύο πλακών. Έτσι θα έχουμε δυναμικές γραμμές μόνο ανάμεσα στις δύο πλάκες με μεγαλύτερη πυκνότητα από ότι πριν. Είναι σαν να μαζέψαμε την ενέργεια του ηλεκτρικού πεδίου που ήταν διασκορπισμένη παντού και να την τοποθετήσαμε στο χώρο ανάμεσα στους οπλισμούς. Να γιατί ο πυκνωτής λειτουργεί σαν μια κονσέρβα ηλεκτρικής ενέργειας.

 

 

Η ηλεκτρική ενέργεια που αποθηκεύεται σε έναν πυκνωτή δίνεται από τη σχέση:

 

U=12QV$U=\frac{1}{2} Q V$

 

Σύμφωνα με τον ορισμό του δυναμικού V=UQ$V=\frac{U}{Q}$ η ηλεκτρική ενέργεια θα έπρεπε να είναι U=Q⋅V$U=Q\cdot V$ . Γιατί μπαίνει στον τύπο αυτό το ½; Αυτό μπορούμε να το καταλάβουμε αν πάρουμε ένα παράδειγμα με τη δυναμική ενέργεια λόγω βάρους. Η σχέση που δίνει τη δυναμική ενέργεια λόγω βάρους είναι η U=mgh. Ας πούμε λοιπόν ότι έχουμε ορισμένα τούβλα που συνολικά έχουν μάζα m και τα ανεβάζουμε στον πρώτο όροφο ενός κτηρίου. Η δυναμική ενέργεια των τούβλων θα είναι mgh. Αν όμως αντί να τα ανεβάσουμε όλα στον πρώτο όροφο τα βάζουμε το ένα πάνω στο άλλο φτιάχνοντας μία στήλη μέχρι τον πρώτο όροφο, η ενέργεια δεν θα είναι mgh αφού για τα πρώτα τούβλα που βρίσκονται στο κάτω μέρος της στήλης κουραστήκαμε πολύ λιγότερο. Η ενέργεια σε αυτή την περίπτωση θα είναι mgh/2 αφού το κέντρο βάρους της στήλης είναι στο μέσον της. Με άλλα λόγια για να δημιουργήσουμε τη στήλη ύψους h κουραστήκαμε ακριβώς το ίδιο που θα κουραζόμασταν αν ανεβάζαμε όλα τα τούβλα στον ημιόροφο που βρίσκεται σε ύψος h/2 αφού όση ενέργεια κερδίζουμε για ένα τούβλο που βρίσκεται στη στήλη σε ύψος χ κάτω από τον ημιόροφο, τόση χάνουμε από το τούβλο που βρίσκεται σε ύψος χ πάνω από τον ημιόροφο.

Το ίδιο ακριβώς συμβαίνει και με τον πυκνωτή, ο οποίος δεν έχει ένα στοιχειώδες φορτίο, αλλά πολλά φορτία τα οποία τοποθετούνται σταδιακά σε αυτόν. Τα πρώτα φορτία μπαίνουν εύκολα. Η φόρτιση γίνεται όλο και πιο δύσκολη υπόθεση, αφού όσο φορτίζεται ο πυκνωτής, τόσο περισσότερο τα φορτία που έρχονται απωθούνται από τα υπάρχοντα φορτία.

 

Ερμηνεία της 2ης ιδιότητας

Όταν ένας πυκνωτής τροφοδοτείται από εναλλασσόμενη τάση, τότε σε χρόνο T/4 φορτίζεται με φορτίο Q0=CV0 όπου V0 το πλάτος της εναλλασσόμενης τάσης. Έτσι έχουμε

I―=Q0T4=4CV0f→V0I¯≈1Cf$\overline{\mathrm{I}}=\frac{Q_{0}}{\frac{T}{4}}=4 C V_{0} f \rightarrow \frac{V_{0}}{\bar{I}} \approx \frac{1}{C f}$

όπου I―$\overline{\mathrm{I}}$ η μέση τιμή του ρεύματος.

Το πηλίκο της μέγιστης τάσης προς το μέσο ρεύμα έχει μονάδες αντίστασης και από φυσικής άποψης εκφράζει και την «αντίσταση» που παρουσιάζει ένας πυκνωτής στην εναλλασσόμενη τάση. Το πηλίκο αυτό δεν είναι ακριβώς η αντίσταση αφού αντίσταση καλούμε το πηλίκο της μέγιστης τάσης προς το μέγιστο ρεύμα, αλλά είναι ανάλογο της αντίστασης. Παρατηρούμε ότι η αντίσταση που παρουσιάζει είναι αντιστρόφως ανάλογη της χωρητικότητας του πυκνωτή και αντιστρόφως ανάλογη της συχνότητας της τάσης. Άρα αν ένας πυκνωτής έχει μεγάλη χωρητικότητα και τροφοδοτείται από εναλλασσόμενη τάση μεγάλης συχνότητας, τότε θα παρουσιάζει πολύ μικρή αντίσταση. Με άλλα λόγια είναι σαν να περνάει το εναλλασσόμενο ρεύμα από τον πυκνωτή χωρίς κανένα εμπόδιο!

Εργαστηριακές δραστηριότητες εμπέδωσης

1. Χρησιμοποιείστε τον πυκνωτή ως αποθήκη ηλεκτρικής ενέργειας.

Σας δίνεται ένας πυκνωτής 1F, μία μπαταρία 9V και ένα λαμπάκι από χριστουγεννιάτικο δένδρο 2W και ένα χρονόμετρο.

Συνδέστε τον πυκνωτή στην μπαταρία. Υπολογίστε το φορτίο και την ενέργεια που θα αποκτήσει ο πυκνωτής. Αποσυνδέστε τον πυκνωτή από την μπαταρία και συνδέστε τον με το λαμπάκι. Μετρήστε το χρόνο για τον οποίο ανάβει το λαμπάκι. Υπολογίστε το χρόνο θεωρητικά. Βρείτε τη διαφορά % ανάμεσα στη θεωρητική και την πειραματική τιμή του χρόνου. Που πιστεύετε ότι οφείλεται αυτή η διαφορά;

2. Φτιάξτε μία Λουγδουνική λάγηνο.

Πριν από αρκετά χρόνια σε κάποιο βιβλίο της φυσική που έδειχνε έναν πυκνωτή κάτω από την εικόνα έγραφε Λουγδουνική Λάγηνος. Σήμερα θα το λέγαμε ποτήρι του Leyden ( πόλη της Ολλανδίας που πρωτοκατασκευάστηκε ο πυκνωτής). Το Λουγδουνική το λέγαμε γιατί παλιότερα την πόλη Leyden τη λέγαμε Λουγδούνον και λάγηνο λέγαμε το ποτήρι.

Τι θα χρειαστείτε. Ένα κουτί από μπαλάκια του τένις, αυτοκόλλητη ταινία αλουμινίου και λίγο σύρμα.

Κολλήστε την αυτοκόλλητη ταινία αλουμινίου στο εσωτερικό και στο εξωτερικό του κουτιού. Κόψτε δύο κομμάτια σύρμα, γυμνώστε τα άκρα τους και στερεώστε το πένα κομμάτι στο εσωτερικό μέρος του ποτηριού και το δεύτερο στο εξωτερικό. Έχετε φτιάξει έναν πυκνωτή. Μπορείτε να φορτίσετε αυτόν το πυκνωτή με μία γεννήτρια Wimshurst. Ο πυκνωτής θα αποκτήσει αρκετά φορτία και ενέργεια τα οποία θα μπορεί να συντηρήσει για αρκετή ώρα. Αν πάνω στο καπάκι του πυκνωτή τοποθετήσετε ένα κέρμα στο κέντρο ενός αλουμινόχαρτου που περιφερειακά υπάρχει άλλο αλουμινόχαρτο συνδεδεμένο με τον άλλο οπλισμό του πυκνωτή, τότε αν κάποιος φίλος σας επιχειρήσει να πάρει το κέρμα, θα δεχθεί ένα ισχυρό ηλεκτρικό σοκ.

 

3. Φτιάξτε έναν επίπεδο πυκνωτή

Θα χρειαστείτε ένα χαρτί A4, αυτοκόλλητη ταινία αλουμινόχαρτου ή απλό αλουμινόχαρτο και σελοτέιπ. Κολλήστε το αλουμινόχαρτο από τη μία και από την άλλη μεριά του χαρτιού το αλουμινόχαρτο.

Έτσι έχετε φτιάξει έναν επίπεδο πυκνωτή. Μετρήστε το μήκος και το πλάτος του χαρτιού Α4 και υπολογίστε το εμβαδόν του.

Μετρήστε το πλάτος του χαρτιού είτε άμεσα με τη βοήθεια ενός παχύμετρου είτε έμμεσα μετρώντας το πάχος όλου του πακέτου των 500 φύλλων.

Αν από τους πίνακες είναι γνωστό ότι η διηλεκτρική σταθερά του χαρτιού είναι 4 βρείτε τη χωρητικότητα του πυκνωτή που φτιάξατε.

Αν βρέξετε το χαρτί πόση θα γίνει η χωρητικότητα;

4. Μελετήστε τη συμπεριφορά του πυκνωτή στο εναλλασσόμενο ρεύμα

Συνδέστε ένα λαμπάκι σε σειρά με έναν πυκνωτή μεγάλης χωρητικότητας. Μπορείτε να χρησιμοποιήσετε έναν ηλεκτρολυτικό πυκνωτή ή τον πυκνωτή που φτιάξατε στην προηγούμενη δραστηριότητα, με βρεγμένο το χαρτί. Τροφοδοτείστε με τη βοήθεια μίας μπαταρίας με σταθερή τάση το σύστημα. Τι παρατηρείτε σχετικά με τη φωτοβολία του λαμπτήρα; Τροφοδοτείστε τώρα το σύστημα με εναλλασσόμενη τάση με τη βοήθεια μίας γεννήτριας συχνοτήτων. Ρυθμίστε τη γεννήτρια συχνοτήτων σε μεγάλη συχνότητα ( 10Khz). Τι παρατηρείτε σχετικά με τη φωτοβολία του λαμπτήρα;

Επιστροφή στην αρχή

Αρχή του θερμομέτρου

Υλικά που θα χρειαστούμε:

1. Δύο μπουκάλια μπύρας
2. Ένα φελλό
3. Μία βελόνα πλεξίματος
4. Μία καρφίτσα
5. Ένα καλαμάκι
6. Ένα βαράκι των 100g
7. Ένα γκαζάκι

Κατασκευή:

Σφηνώνουμε το φελλό στο ένα μπουκάλι. Το ένα άκρο της βελόνας ( τη μύτη) το σφηνώνουμε στο φελλό και το άλλο το στηρίζουμε στο άλλο μπουκάλι. Στην άκρη της βελόνας βάζουμε το βαράκι. Στο μπουκάλι που είναι το βαράκι, βάζουμε ανάμεσα στο μπουκάλι και στη βελόνα την καρφίτσα. Κόβουμε ένα κομμάτι από το καλαμάκι και στο μέσον του το τοποθετούμε στην καρφίτσα ώστε να αποτελέσει τον δείκτη του θερμομέτρου μας. Η συσκευή μας είναι έτοιμη.

Λειτουργία:

Ζεσταίνοντας με το γκαζάκι τη βελόνα πλεξίματος αυτή διαστέλλεται. Επειδή από τη μια μεριά είναι πακτωμένη στο φελλό η διαστολή θα προχωρήσει προς την άλλη παρασύροντας σε κύλιση την καρφίτσα. Όπως κυλίεται η καρφίτσα περιστρέφεται ο δείκτης – καλαμάκι που είναι καρφιτσωμένος πάνω της.

Μερικές παρατηρήσεις για την κατασκευή

Το βαράκι μπαίνει ώστε να αυξηθεί η κάθετος δύναμη που ασκείται στην καρφίτσα. Έτσι αυξάνεται και η δύναμη της στατικής τριβής και δεν γλιστράει η βελόνα πάνω στην καρφίτσα

Αν η γωνία περιστροφής της καρφίτσας είναι πχ φ (rad), η καρφίτσα, άρα και η βελόνα θα έχουν μετακινηθεί κατά s=φR όπου R η ακτίνα της καρφίτσας. Γι αυτό βάλαμε καρφίτσα ώστε για δεδομένο s να έχουμε μεγάλη γωνία περιστροφής αφού η ακτίνα της καρφίτσας είναι μικρή.

Αν μετρήσουμε τη διάμετρο της καρφίτσας το μήκος της βελόνας και τη γωνία περιστροφής και δεδομένου ότι α=12x10-6C-1 μπορούμε να προβούμε σε ποσοτικούς υπολογισμούς

http://youtu.be/igdHvcGD21U

Επιστροφή στην αρχή

Κατασκευή μίας πολύ απλής μηχανής του Ήρωνα

Κατασκευή μίας συσκευής Hofman

Κατασκευή μανόμετρου με απλά υλικά

Κατασκευή αισθητήρα θερμοκρασίας για πολύμετρο -βρασμός

Επιστροφή στην αρχή