Μετρήσεις Σφάλματα & αβεβαιότητες

Σφάλμα & αβεβαιότητα

Το σφάλμα και η αβεβαιότητα αποτελούν δυο έννοιες οι οποίες δημιουργούν πολύ συχνά σύγχυση και είναι δυσδιάκριτα τα όρια τους. Συχνά η μια έννοια χρησιμοποιείται στην θέση της άλλης.

Η κύρια διαφορά μεταξύ σφαλμάτων και αβεβαιοτήτων είναι:

· το σφάλμα είναι η διαφορά μεταξύ της πραγματικής τιμής (κοινά αποδεκτή πρότυπη τιμή) και της μετρούμενης τιμής. Το σφάλμα συνδέεται με την ακρίβεια της μέτρησης.

· H αβεβαιότητα είναι μια παράμετρος, η οποία συσχετίζεται με το αποτέλεσμα της μέτρησης μιας φυσικής ποσότητας, και η οποία χαρακτηρίζει την διασπορά των τιμών (εκτίμηση ενός εύρους τιμών) που μπορούν λογικά να αποδοθούν ‐ αντιστοιχηθούν στην φυσική ποσότητα.

Στην ευρύτερη έννοιά της, η «αβεβαιότητα μιας μέτρησης» εκφράζει τις αμφιβολίες μας σχετικά με την ακρίβεια και την ορθότητα του αποτελέσματος μιας μέτρησης και συνιστά την αξιοπιστία της συγκεκριμένης μέτρησης. Ωστόσο η αξιοπιστία δεν είναι ικανή συνθήκη για καλή ακρίβεια και μπορεί να απέχει πολύ από την όντως πραγματική τιμή (πρότυπη τιμή) αν υπάρχουν σημαντικά συστημικά σφάλματα.

Στο παρακάτω σχήμα φαίνεται η διάφορα των εννοιών. Έχω ένα χάρακα ο όποιος δεν είναι πολύ καλά βαθμονομημένος και μετρώ το μήκος μιας σελίδας Α4 με ακρίβεια χιλιοστού και με τιμές: 31.4 , 31.5, 31.6 ενώ η πραγματική τιμή είναι 29.7.

Η ακρίβεια (accuracy) αναγράφεται ποσοτικά χρησιμοποιώντας το σχετικό σφάλμα

Η αξιοπιστία (precision) αναγράφεται ποσοτικά χρησιμοποιώντας την σχετική η κλασματική αβεβαιότητα

Παράδειγμα

Ας υποθέσουμε ότι μετράμε την αντίσταση ενός υλικού. Οι μετρούμενες τιμές δεν θα είναι ποτέ ίδιες επειδή οι μετρήσεις αντίστασης ποικίλλουν. Γνωρίζουμε ότι υπάρχει μια αποδεκτή τιμή 3,4 ohms και μετρώντας την αντίσταση δύο φορές, λαμβάνουμε τα αποτελέσματα 3,35 και .

Τα τυχόν σφάλματα παρήγαγαν τις τιμές 3.35 (σφάλμα 0.05) και 3.41(σφάλμα 0.01), ενώ το εύρος μεταξύ 3.35 και 3.41 είναι το εύρος αβεβαιότητας (0.06).

Παράδειγμα

Η τυπική επιτάχυνση βαρύτητας είναι . Στο εργαστήριο, πραγματοποιώντας κάποια πειράματα χρησιμοποιώντας ένα εκκρεμές, λαμβάνουμε τέσσερις τιμές για το g:

και

Η διακύμανση των παραπάνω τιμών είναι προϊόν σφαλμάτων. Η μέση τιμή είναι:

.

Το εύρος αβεβαιότητας για τις μετρήσεις φτάνει από , έως (0.3) ενώ η απόλυτη αβεβαιότητα είναι περίπου ίση με το μισό του εύρους μας, το οποίο είναι ίσο με τη διαφορά μεταξύ της μέγιστης και της ελάχιστης τιμής διαιρούμενη με δύο .

Η απόλυτη αβεβαιότητα αναφέρεται ως εξής:

Σε αυτή την περίπτωση, θα είναι:

ή

Όταν κάνετε μετρήσεις, πρέπει να αναφέρεται την αβεβαιότητα. Βοηθά όσους διαβάζουν τα αποτελέσματα να γνωρίζουν την πιθανή διακύμανση που μπορεί να έχει η τιμή.

Εκτίμηση αβεβαιότητας

Τύπου Β

1. όριο σφάλματος του οργάνου (Instrument Limit of Error) ILE.

2. άλλες αβεβαιότητες όταν είναι μεγαλύτερες από το ILE.

Τύπου Α

3. εκτίμηση της αβεβαιότητας με επαναλαμβανόμενες μετρήσεις και στατιστική ανάλυση

1) Όριο σφάλματος του οργάνου

Το όριο σφάλματος του οργάνου (ILE) είναι η ακρίβεια με την οποία μπορεί να διαβαστεί μια συσκευή μέτρησης και είναι πάντα ίση ή μικρότερη από την ελάχιστη μέτρηση. Το Όριο Σφάλματος του Οργάνου (Instrument limit error)(ILE) γενικά θεωρείται ότι είναι η ελάχιστη μέτρηση (Least Count) ή κάποιο κλάσμα (1/2, 1/5, 1/10) της ελάχιστης μέτρησης χωρίς να υπάρχουν αυστηροί κανόνες για την επιλογή. Εάν το διάστημα μεταξύ των διαιρέσεων της κλίμακας είναι μεγάλο, μπορεί να είστε άνετοι στην εκτίμηση στο 1/5 ή το 1/10 της ελάχιστης μέτρησης. Εάν οι διαιρέσεις της κλίμακας είναι πιο κοντά μεταξύ τους, ενδέχεται να μπορείτε να υπολογίσετε μόνο στο πλησιέστερο 1/2 της ελάχιστης μέτρησης και εάν οι διαιρέσεις της κλίμακας είναι πολύ κοντά, ενδέχεται να μπορείτε να υπολογίσετε μόνο τη μικρότερη μέτρηση.

Αναλογικά όργανα

Κατά την καταγραφή μιας μέτρησης συμπεριλαμβάνουμε όλα τα γνωστά ψηφία που μπορούμε να διακρίνουμε συν ένα τελικό εκτιμώμενο ψηφίο (αβέβαιο ψηφίο).

Στον πρώτο χάρακα από κάτω σημειώνονται τα cm οπότε μπορούμε να καταγράψουμε το 2. Αλλά πρέπει επίσης να υπολογίσουμε ένα και μόνο ένα επιπλέον ψηφίο. Έτσι σε αυτή την περίπτωση μπορεί να καταγράψουμε 2,3 cm ή ίσως 2,4 cm. Οποιοδήποτε από τα δύο θα ήταν σωστό καθώς το 2 (θέση ενός) είναι επακριβώς γνωστό ενώ το τελικό ψηφίο (θέση δέκατα) εκτιμάται.

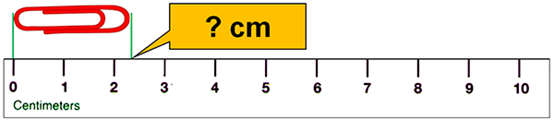
Εικόνα 1. Χάρακας με ακρίβεια cm.

Στον δεύτερο χάρακα σημειώνονται τόσο τα cm όσο και τα mm που σημαίνει ότι μπορούμε να δούμε καθαρά ότι το πρώτο μέρος της μέτρησης είναι 2,3. Ωστόσο, πρέπει και πάλι να υπολογίσουμε ένα επιπλέον ψηφίο ή θέση π.χ. 2,35 cm.

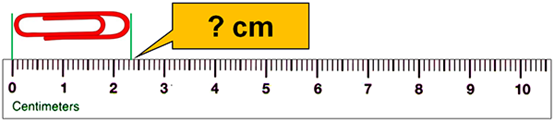
Εικόνα 2.Χάρακας με ακρίβεια mm.

Η ελάχιστη καταμέτρηση είναι η μικρότερη διαίρεση που σημειώνεται στο όργανο. Έτσι, ένας χάρακας μπορεί θα έχει ελάχιστο μέτρημα 1,0 mm, ένα ψηφιακό ρολόι μπορεί να έχει ελάχιστο μέτρημα 0,01 sec.

Ψηφιακά όργανα

Στα ψηφιακά όργανα το τελευταίο ψηφίο εκλαμβάνεται ως αβέβαιο.

Παρατήρηση για ψηφιακά πολύμετρα (ΨΠ)

Οι αβεβαιότητες για τα ΨΠ αναφέρονται πάντα ως ποσοστό της ένδειξης συν κάποιο ακέραιο-πολλαπλάσιο του λιγότερο σημαντικού ψηφίου (dgt) στην κλίμακα. π.χ. ±(2,5% + 3 dgt)

Έτσι, για παράδειγμα, αν μετρήσουμε μια τάση 32,00 V σε μια κλίμακα που έχει την αβεβαιότητα που αναφέρεται παραπάνω (όπου το 0,01 V είναι το λιγότερο σημαντικό ψηφίο σε αυτήν την κλίμακα), τότε η απόλυτη αβεβαιότητα της μέτρησής μας θα είναι:

(32,00 × 0,025) = 0,8

+ (3 × 0,01) = 0,03

= 0,83 ⇒ ±0,8V

Παρατηρήστε πώς το 3× (το λιγότερο σημαντικό ψηφίο) συνέβαλε αμελητέα στη συνολική αβεβαιότητα σε αυτό το παράδειγμα. Ωστόσο, αν μετρήσουμε μια τάση 0,09 V στην ίδια κλίμακα, τότε η απόλυτη αβεβαιότητα θα είναι:

(0,09 × 0,025) = 0,00225

+ (3 × 0,01) = 0,03

= 0,03225 ⇒ 0,03V

Αυτό δείχνει γιατί είναι σημαντικό να χρησιμοποιείτε την πιο ευαίσθητη κλίμακα στο ΨΠ που θα εξακολουθεί να μετράει την ανάγνωσή σας. Σε αυτήν την περίπτωση, το 3× (το λιγότερο σημαντικό ψηφίο) ήταν η κύρια συμβολή και μας έδωσε μια αβεβαιότητα που είναι πολύ μεγάλη σε σύγκριση με την αξία μας. Η χρήση μιας πιο ευαίσθητης κλίμακας θα μας δώσει μια καλύτερη (δηλαδή μικρότερη) αβεβαιότητα.

2) Εκτίμηση πραγματικής τιμής μέσω άλλων παραμέτρων

· Συχνά άλλες αβεβαιότητες είναι μεγαλύτερες από το Όριο Σφάλματος του Οργάνου. Μπορεί να προσπαθήσουμε να εξισορροπήσουμε μια απλή ζυγαριά με μάζες που έχουν ILE 0,01 γραμμάρια, αλλά διαπιστώνουμε ότι μπορούμε να αλλάξουμε τη μάζα έως και 3 γραμμάρια χωρίς να δούμε αλλαγή στον δείκτη. Θα χρησιμοποιούσαμε το μισό από αυτό ως την εκτιμώμενη αβεβαιότητα, λαμβάνοντας έτσι αβεβαιότητα ±1,5 γραμμάρια.

· Ένα άλλο καλό παράδειγμα είναι ο προσδιορισμός της εστιακής απόστασης ενός φακού μετρώντας την απόσταση από τον φακό στην οθόνη. Το ILE μπορεί να είναι 0,1 cm, ωστόσο το βάθος πεδίου μπορεί να είναι τέτοιο ώστε η εικόνα να παραμένει εστιασμένη ενώ μετακινούμε την οθόνη κατά 1,6 cm. Σε αυτήν την περίπτωση η εκτιμώμενη αβεβαιότητα θα ήταν το μισό του εύρους ή ±0,8 cm.

3) Εκτίμηση Τυπικής Αβεβαιότητας - τυπικού σφάλματος

Η τυπική αβεβαιότητα εκφράζεται μέσω του τυπικού σφάλματος στη μέση τιμή και μας δείχνει μια εκτίμηση για το σφάλμα που έχει η μέση τιμή των μετρήσεων μας, την οποία θεωρούμε ως καλύτερη εκτίμηση της πραγματικής τιμής. Για να γίνει αυτό, πρέπει να κάνετε τα εξής βήματα:

· Υπολογίστε το μέσο όρο όλων των μετρήσεων,

· Υπολογίστε την τυπική απόκλιση (για δείγμα)

· Υπολογίστε το τυπικό σφάλμα του μέσου όρου,

Οπότε x=± SE

Εναλλακτικά ως μια απλούστερη διαδικασία μπορούμε να χρησιμοποιήσουμε την τυπική απόκλιση s η για περισσότερη απλότητα την μέση απόκλιση

Οπότε x=±s ή x=± MD

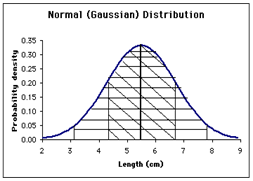
Παρατήρηση

Γενικά οι αποδέκτες τιμές του x βρίσκονται σε διάστημα 2 τυπικών αποκλίσεων (επίσης για απλότητα, προσεγγιστικά μέσων απολυτών αποκλίσεων). Αυτό συμβαίνει διότι θεωρούμε ότι τα τυχαία σφάλματα ακολουθούν σε γενικές γραμμές την κανονική κατανομή όπως δείχνεται στο παρακάτω σχήμα. Το 68% των μετρήσεων βρίσκονται μεταξύ 1 τυπικών αποκλίσεων ενώ το 95% μεταξύ 2 τυπικών αποκλίσεων. Στις 3 αποκλίσεις έχουμε το 99%. Τα ποσοστά αυτά ονομάζονται διαστήματα εμπιστοσύνης (confidence interval) και δίνονται μαζί με την αβεβαιότητα.

Αν υποθέσουμε ότι μετράμε την πυκνότητα του ασβεστίτη ως (2,65 ± 0,04) και η τιμή του σχολικού βιβλίου είναι 2,71 θα μπορούσαμε να ισχυριστούμε ότι συμφωνούν οι δύο τιμές;

Η τιμή 2,65 είναι εντός του εύρους δύο αποκλίσεων από τη μέση τιμή που μετράμε, οπότε μπορούμε να ισχυριστούμε ότι η τιμή μας συμφωνεί με το βιβλίο και είναι αποδεκτή.

Εάν είχαμε μετρήσει την πυκνότητα σε (2,65 ± 0,01) τοτε θα αναγκαζόμασταν να παραδεχτούμε ότι η τιμή μας διαφωνεί με το βιβλίου και δε είναι αποδεκτή.

Παραδείγματα

Ως παράδειγμα χρησιμοποιούμε τον Πίνακας 1. Η στήλη 1 περιέχει τις μετρήσεις του χρόνου της περιόδου ενός εκκρεμούς σε δευτερόλεπτα, και έτσι υπολογίζουμε την μέση απόκλιση καθώς και την τυπική απόκλιση τον δείγματος μας. Η ακρίβεια του χρονομέτρου είναι 0.1 s και έχω δυο σημαντικά ψηφία.

Πίνακας 1. Χρόνος ταλάντωσης εκκρεμούς

Time, t, sec.	|t - |, sec	(t-)^2
7.4	0.2	0.04
8.1	0.5	0.25
7.9	0.3	0.09
7.0	0.6	0.36
	MD=

Με βάση τον παραπάνω πίνακα μπορώ να κάνω τις εξής εκτιμήσεις για το μέγεθός t:

· Η εκτίμηση που έχω για το μέγεθος t μπορεί να είναι t= ± MD.

Δηλαδή t= (7.6 ± 0,4) sec.

εναλλακτικά

· Η εκτίμηση που έχω για το μέγεθος t μπορεί να είναι t= ± s.

Δηλαδή t=(7.6 ± 0,5) sec.

Στην περίπτωση που μετράμε την πυκνότητα πλαστελίνης η ακρίβεια της ζυγαριάς είναι 0.01 g και του σωλήνα 1ml. Το τελευταίο ψηφίο της ζυγαριάς είναι το αβέβαιο ψηφίο ενώ για τον σωλήνα σημειώνουμε την ένδειξη που ξεπερνιέται από τη στάθμη του νερού και εκτιμάμε το μισό της κλίμακας. Εάν π.χ. δείχνει μεταξύ 80 και 81 θα πάρουμε ως μετρήσιμη τιμή το 80.5 με αβέβαιο το 5.

Μάζα (m)	Όγκος (V)	Πυκνότητα (d)
20.22	80-70=10.5	1.926≈1.93 (3 ΣΨ & ΣΤΡ)
26.15	82-70=12.5	2.092≈2.09 (3 ΣΨ & ΣΤΡ)
29.11	84-70=14.5	2.079≈2.08 (3 ΣΨ & ΣΤΡ)
24.30	81-70=11.5	2.113≈2.11 (3 ΣΨ & ΣΤΡ)

(αβεβαιότητα)

Μπορούμε άραγε να μετρήσουμε την πυκνότητα της πλαστελίνης με μεγαλύτερη ακρίβεια με τα ίδια ακριβώς όργανα; Η απάντηση είναι ναι.

Αρκεί να μετρήσουμε μεγαλύτερες ποσότητες. Αν πχ πάρουμε ένα κομμάτι πλαστελίνης και μετρήσουμε την μάζα m=351,32 g και τον όγκο V=166ml παρατηρούμε ότι το αποτέλεσμα θα πρέπει να το δώσουμε με 3 ψηφία αυτή τη φορά, αφού τόσα είναι τα λιγότερα σημαντικά ψηφία του όγκου. Άρα η πυκνότητα θα είναι 2,12 g/mL και η τιμή θα έχει μεγαλύτερη αξιοπιστία.

Το συμπέρασμα είναι ότι η αξιοπιστία της μέτρησης αυξάνεται (οπότε ελαττώνεται η αβεβαιότητα) όσο μεγαλύτερο είναι το μετρούμενο μέγεθος σε σύγκριση με την κλίμακα-ακρίβεια του οργάνου, όταν δηλαδή μειώνεται η σχετική αβεβαιότητα.

Έτσι για τη μέτρηση της πυκνότητας, είναι λάθος μεθοδολογία να χρησιμοποιήσουμε σφαιρικά κομμάτια πλαστελίνης όπως προτείνεται σε πολλούς εργαστηριακούς οδηγούς, αφού τότε ο όγκος της πλαστελίνης είναι συγκρίσιμός με την κλίμακα μέτρησης του ογκομετρικού κυλίνδρου. Για μεγαλύτερη ακρίβεια του πειράματος θα πρέπει να χρησιμοποιήσουμε κυλινδρικά κομμάτια πλαστελίνης όσο δυνατό μεγαλύτερου όγκου.

Συζήτηση

Γενικός κανόνας είναι ότι κατά την διάρκεια των μετρήσεων θα πρέπει να αποφεύγουμε να είναι μεγάλες οι σχετικές αβεβαιότητες. Τι σημαίνει αυτό;

Δεν μπορώ να μετρώ τον όγκο μικρών κομματιών με ογκομετρικό σωλήνα διότι αν ο όγκος μετράται 2ml και η αβεβαιότητα είναι 1 ml τότε το επί τοις εκατό σχετική αβεβαιότητα είναι .

Το ίδιο κάνω κατά την μέτρηση ενός εκκρεμούς. Δεν μπορώ να μετρήσω εύκολα μικρές περιόδους διότι η χρονική αβεβαιότητα είναι σημαντική. Στην περίπτωση του εκκρεμούς η αβεβαιότητα ίσως δεν εξαρτάται μόνο από τη αξιοπιστία του οργάνου άλλα ίσως είναι πολλαπλάσια, αφού υπεισέρχονται παράγοντες όπως η όραση μας η οποία δεν μπορεί να διακρίνει επακριβώς την αρχή και το τέλος της μέτρησης.

Παράδειγμα

Τι μπορώ να κάνω;

· Είτε να μετρήσω μεγαλύτερους όγκους π.χ. 40ml οπότε η σχετική αβεβαιότητα θα είναι .

· Είτε στην περίπτωση του εκκρεμούς να μετρήσω πολλές ταλαντώσεις π.χ. N ταλαντώσεις κι να κάνω εκτίμηση της περιόδου Τ διαιρώντας με το N, .

Η σχετική αβεβαιότητα της περιόδου μέσω της έμμεσης μέτρησης μειώνεται επίσης και είναι . Π.χ. εάν σε 10 ταλαντώσεις t=30 sec 2 sec, τότε η αβεβαιότητα στην περίοδο μπορούμε να πούμε ότι είναι T=30.2, .

Εάν παίρναμε ξεχωριστές μετρήσεις τότε θα είχαμε T=32 δηλαδή σχετική αβεβαιότητα πολύ μεγάλη,

Τι είναι η βαθμονόμηση και η ανοχή;

· Η ανοχή(tolerance) είναι το εύρος μεταξύ της μέγιστης και της ελάχιστης επιτρεπόμενης τιμής για μια μέτρηση. Ανοχή διαμέτρου ενός κυλίνδρου για πιστόνι.

· Βαθμονόμηση (calibration) είναι η διαδικασία συντονισμού ενός οργάνου μέτρησης έτσι ώστε όλες οι μετρήσεις να εμπίπτουν στο εύρος ανοχής. Για τη βαθμονόμηση ενός οργάνου, τα αποτελέσματά του συγκρίνονται με άλλα όργανα με μεγαλύτερη ακρίβεια και ακρίβεια ή με ένα αντικείμενο του οποίου η τιμή έχει πολύ υψηλή ακρίβεια. Ένα παράδειγμα είναι η βαθμονόμηση μιας ζυγαριάς, ενός θερμομέτρου κτλ.

Διάδοσή αβεβαιότητας μέσω α) διακύμανσης και β) σημαντικών ψηφίων

Διάδοση Διακύμανσης

Έστω μέγεθος με τιμή μέτρησης z τότε, συμβολίζουμε με Δz το απόλυτο σφάλμα ενώ με το σχετικό σφάλμα ή κλασματική αβεβαιότητα.

Ο συνδυασμός φυσικών μεγεθών επηρεάζει το συνολικό σφάλμα. Πιο συγκεκριμένα:

Πρόσθεση μεγεθών

Πολλαπλασιασμός μεγέθους με αριθμό

Πολλαπλασιασμός & διαίρεση μεγεθών

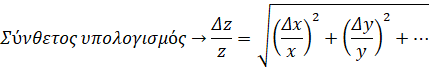
Μέγεθος σε Δύναμη

Τα Δx , Δy αποτελούν τα σφάλματα μέτρησης των επιμέρους φυσικών μεγεθών.

Διάδοση με σημαντικά ψηφιά

Οι κανόνες για τη διάδοση των σφαλμάτων ισχύουν για περιπτώσεις που βρισκόμαστε στο εργαστήριο, αλλά η διάδοση των σφαλμάτων είναι χρονοβόρα. Οι κανόνες για σημαντικά ψηφία επιτρέπουν σε μια πολύ πιο γρήγορη μέθοδο να ληφθούν αποτελέσματα που είναι περίπου σωστά ακόμα και όταν δεν έχουμε τιμές αβεβαιότητας. Αξίζει να θυμηθούμε ότι κάθε φορά που κάνετε μια μέτρηση, ο αριθμός των σημαντικών ψηφίων που σημειώνετε υποδηλώνει το σφάλμα στη μέτρηση.

Σημαντικά ψηφία και κανόνες για τον προσδιορισμό τους

02-SimantikaPsifia-eClass.pdf (aspete.gr)

Α. Μετρώντας τα σημαντικά ψηφιά

· 23.5 – Τρία σημαντικά ψηφία, καθώς όλα είναι μη μηδενικοί αριθμοί.

· 23.50 – Τέσσερα σημαντικά ψηφία. Το τελικό μηδέν είναι σημαντικό επειδή ο αριθμός περιέχει δεκαδικά ψηφία.

· 402 – Τρία σημαντικά ψηφία. Το μηδέν βρίσκεται μεταξύ μη μηδενικών αριθμών.

· 5200 – Δύο σημαντικά ψηφία. Δεν υπάρχει δεκαδικό ψηφίο, επομένως τα μηδενικά στο τέλος είναι απλώς σύμβολα θέσης και δεν είναι σημαντικά.

· 0,030 – Δύο σημαντικά ψηφία. Τα προηγούμενα μηδενικά δεν είναι ποτέ σημαντικά. Το μηδέν που ακολουθεί είναι σημαντικό επειδή ο αριθμός περιέχει δεκαδικό ψηφίο

· 0,0070080 – Πέντε σημαντικά ψηφία. Τα προηγούμενα μηδενικά δεν είναι ποτέ σημαντικά. Τα δύο μηδενικά μεταξύ 7 και 8 είναι σημαντικά επειδή βρίσκονται μεταξύ μη μηδενικών αριθμών. Το μηδέν που ακολουθεί είναι σημαντικό επειδή ο αριθμός περιέχει δεκαδικά ψηφία.

Περιπτώσεις για προσοχή

Ο προσδιορισμός των σημαντικών αριθμών σε έναν αριθμό απαιτεί να γνωρίζουμε ποια ψηφία είναι αξιόπιστα (π.χ. γνωρίζοντας τη μέτρηση ή την ανάλυση με την οποία λαμβάνεται ή επεξεργάζεται ο αριθμός), καθώς μόνο αξιόπιστα ψηφία μπορούν να είναι σημαντικά. π.χ., 3 και 4 σε 0,00234 g δεν είναι σημαντικά εάν το μετρήσιμο μικρότερο βάρος είναι 0,001 g.

α) 1.79 ± 0.06 (correct)

β) 1.79 ± 0.96 (correct)

γ) 1.79 ± 0.067 (incorrect)

Για παράδειγμα, στο 1,79 ± 0,067 (λανθασμένο), δεν έχει νόημα να έχουμε ακριβέστερη αβεβαιότητα από την καλύτερη εκτίμηση.

Το 1,79 ± 0,96 (λανθασμένο) επίσης δεν έχει νόημα, καθώς η κατευθυντήρια γραμμή στρογγυλοποίησης για την πρόσθεση και την αφαίρεση παρακάτω λέει ότι οι άκρες του εύρους πραγματικών τιμών είναι 2,7 και 0,9 (2,69-0.89=1.8) που είναι λιγότερο ακριβείς από την καλύτερη εκτίμηση 1,79.

Β. Κανόνας για την πρόσθεση και την αφαίρεση σημαντικών ψηφίων

Όταν προστίθενται ή αφαιρούνται μετρήσεις, ο αριθμός των δεκαδικών ψηφίων στην τελική απάντηση πρέπει να ισούται με τον μικρότερο αριθμό δεκαδικών ψηφίων οποιουδήποτε όρου.

256,5895 g + 8,1 g M = 264,6895 g M -> 264,7 g

Γ. Κανόνας πολλαπλασιασμού/διαίρεσης σημαντικών αριθμών

Όταν οι μετρήσεις πολλαπλασιάζονται ή διαιρούνται, ο αριθμός των σημαντικών ψηφίων στην τελική απάντηση θα πρέπει να είναι ίδιος με τον όρο με τον μικρότερο αριθμό σημαντικών ψηφίων.

L1=2,2 cm

L2=38,2935 cm

A=L1 L2=84,126900000 cm² A=84 cm2

Κανόνες στρογγυλοποίησης

Γραφικές παραστάσεις